题目内容
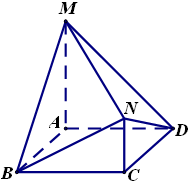如图，正方形ABCD的边长为2，MA，NC都垂直于平面ABCD，且MA=2NC=2．（Ⅰ）证明：MC⊥BD；
（Ⅱ）求直线BN与平面ACNM所成角的正弦值．
分析：（1）连接BD交AC于点O，只需证明BD⊥平面ACNM；
（2）连接ON，可证∠ONB为直线BN与平面ACNM所成角，通过解直角三角形可求；
（2）连接ON，可证∠ONB为直线BN与平面ACNM所成角，通过解直角三角形可求；
解答：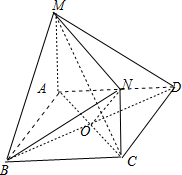
证明：（1）连接BD交AC于点O，
∵ABCD为正方形，∴BD⊥AC，
∵MA⊥平面ABCD，∴MA⊥BD，
又MA∩AC=A，∴BD⊥平面ACNM，
MC?平面ACNM，∴BD⊥AC；
（2）连接ON，由（1）知，BO⊥平面ACNM，
∴∠ONB为直线BN与平面ACNM所成角，
在Rt△BCN中，BN=
，在Rt△BON中，BO=
，
所以sin∠ONB=
，即直线BN与平面ACNM所成角的正弦值为
；
证明：（1）连接BD交AC于点O，∵ABCD为正方形，∴BD⊥AC，
∵MA⊥平面ABCD，∴MA⊥BD，
又MA∩AC=A，∴BD⊥平面ACNM，
MC?平面ACNM，∴BD⊥AC；
（2）连接ON，由（1）知，BO⊥平面ACNM，
∴∠ONB为直线BN与平面ACNM所成角，
在Rt△BCN中，BN=
| 5 |
| 2 |
所以sin∠ONB=
| ||
| 5 |
| ||
| 5 |
点评：本题考查线面角的求解、空间两直线垂直的证明，属中档题．
练习册系列答案
相关题目
如图，正方形ABCD和四边形ACEF所在的平面互相垂直，CE⊥AC，EF∥AC，AB=
8、如图把正方形ABCD沿对角线BD折成直二面角，对于下面结论：
如图，正方形ABCD、ABEF的边长都是1，而且平面ABCD、ABEF互相垂直，点M在AC上移动，点N在BF上移动，若CM=BN=a（0＜a＜
如图，正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD，AE⊥平面CDE．
（2010•温州二模）如图，正方形ABCD与正方形CDEF所成的二面角为60°，则直线EC与直线AD所成的角的余弦值为