题目内容
已知函数f (x)=4sinx•sin2(| π |
| 4 |
| x |
| 2 |
(1)求a的值和f (x)的值域;
(2)设w>0,若y=f (wx)在区间[-
| π |
| 2 |
| 2π |
| 3 |
(3)设|θ|<
| π |
| 2 |
分析:首先将函数化简(1)根据函数是奇函数求出a的值,然后有正弦函数求出值域;
(2)写出函数f (wx)的式子,然后根据正弦函数的单调性求出x的范围,进而根据区间[-
,
]的增函数,求出w的取值范围;
(3)首先求出4+f (x+θ)f (x-θ)并化简和求出最小值
,再利用sin2θ<
,求出结果.
(2)写出函数f (wx)的式子,然后根据正弦函数的单调性求出x的范围,进而根据区间[-
| π |
| 2 |
| 2π |
| 3 |
(3)首先求出4+f (x+θ)f (x-θ)并化简和求出最小值
| 3 |
| 4 |
| 3 |
| 4 |
解答:解:化简得f(x)=2sinx+a+3
(1)f(-x)=-f(x)?a=-3∴f(x)=2sinx
f(x)∈[-2,2](4分)
(2)f(wx)=2sinwx(w>0)
-
+2kπ≤wx≤2kπ+
k∈Z
-
+
≤x≤
+
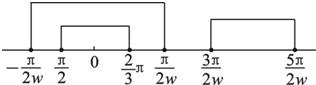
?0<w≤
综上以上,0<w≤
(8分)
(3)|θ|<
,x∈R时
4+4sin(x+θ)sin(x-θ)>4sinx
即sin2x-sinx+1>sin2θ恒成立
(sin2x-sinx+1)min=
∴sin2θ<
-
<sinθ<
θ∈(-
,
)
∴θ∈(-
,
)(13分)
(1)f(-x)=-f(x)?a=-3∴f(x)=2sinx
f(x)∈[-2,2](4分)
(2)f(wx)=2sinwx(w>0)
-
| π |
| 2 |
| π |
| 2 |
-
| π |
| 2w |
| 2kπ |
| w |
| kπ |
| w |
| π |
| 2w |

|
| 3 |
| 4 |
综上以上,0<w≤
| 3 |
| 4 |
(3)|θ|<
| π |
| 2 |
4+4sin(x+θ)sin(x-θ)>4sinx
即sin2x-sinx+1>sin2θ恒成立
(sin2x-sinx+1)min=
| 3 |
| 4 |
∴sin2θ<
| 3 |
| 4 |
-
| ||
| 2 |
| ||
| 2 |
| π |
| 2 |
| π |
| 2 |
∴θ∈(-
| π |
| 3 |
| π |
| 3 |
点评:本题考查了正弦函数的单调性和奇偶性以及不等式恒成立问题,对于不等式恒成立问题转化成求函数最值问题即可.属于中档题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|