Question

在△ABC中，a，b，c分别为角A，B，C的对边，若ccosB=bcosC，且cosA=，则sinB等于________．

Answer 1

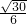
分析：利用正弦定理将（边之比）转化为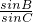（对应角的正弦之比），逆用两角差的正弦可判断出B=C，从而利用半角公式即可求得答案．
解答：由ccosB=bcosC可得=，
由正弦定理知，=，
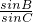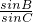∴=，化简得sinBcosC-cosBsinC=0，即sin（B-C）=0，
∴B=C，
∴sinB=sin=cos==．
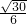故答案为：．
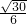点评：本题考查正弦定理、两角差的正弦及二倍角的余弦，求得B=C是关键，考查转化与运算能力，属于中档题．