题目内容
已知函数
(Ⅰ)若函数 在[1,2]上是减函数,求实数a的取值范围;
在[1,2]上是减函数,求实数a的取值范围;
(Ⅱ)令 是否存在实数a,当
是否存在实数a,当 (e是自然常数)时,函数
(e是自然常数)时,函数 的最小值是3,若存在,求出a的值;若不存在,说明理由;
的最小值是3,若存在,求出a的值;若不存在,说明理由;
(Ⅲ)当 时,证明:
时,证明: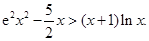
【答案】
(1) (2)存在实数
(2)存在实数 ,使得当
,使得当 时,g(x)有最小值3. (3)略
时,g(x)有最小值3. (3)略
【解析】(I) 函数 在[1,2]上是减函数转化为
在[1,2]上是减函数转化为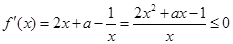 在[1,2]上恒成立,即
在[1,2]上恒成立,即 在[1,2]上恒成立,再利用二次函数的性质,问题得解.
在[1,2]上恒成立,再利用二次函数的性质,问题得解.
(II)利用导数研究其极值最值,在具体求解的过程中,要对a进行讨论.
(III) 构造函数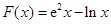 ,结合第(II)问可知
,结合第(II)问可知 ,令
,令 ,只需要满足
,只需要满足 即可.再利用导数研究
即可.再利用导数研究 的最大值.问题得解.
的最大值.问题得解.
解:(Ⅰ)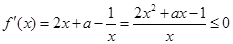 在[1,2]上恒成立,
在[1,2]上恒成立,
令 ,有
,有 得
得 …………3分
…………3分
所以 .
…………4分
.
…………4分
(Ⅱ)假设存在实数a,使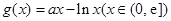 有最小值3,
有最小值3,
 .
…………5分
.
…………5分
①当 时,g(x)在[0,e]上单调递减,
时,g(x)在[0,e]上单调递减,
 (舍去).
(舍去).
(2)当 时,g(x)在
时,g(x)在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,
所以 ,满足条件.
,满足条件.
(3)当 时,g(x)在[0,e]上单调递减,
时,g(x)在[0,e]上单调递减, (舍去).
(舍去).
综上,存在实数 ,使得当
,使得当 时,g(x)有最小值3.
…………10分
时,g(x)有最小值3.
…………10分
(Ⅲ)令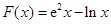 ,由(2)知
,由(2)知
 ,令
,令 ,
, ,
,
当 时,
时, ,
,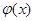 在
在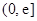 上单调递增,
上单调递增,
所以 .
.
所以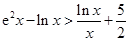 ,即
,即 .
.

练习册系列答案
相关题目
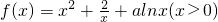 ,
,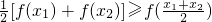 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”. ,
, 成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函 数”.试证当a≤0时,f(x)为“凹函数”.