题目内容
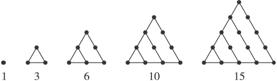
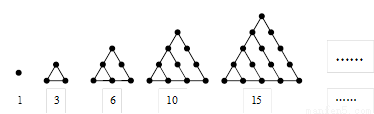
在古希腊,毕达哥拉斯学派把1,3,6,10,15,21,28,…,这些数叫做三角形数,其通项为 ,前n项和为
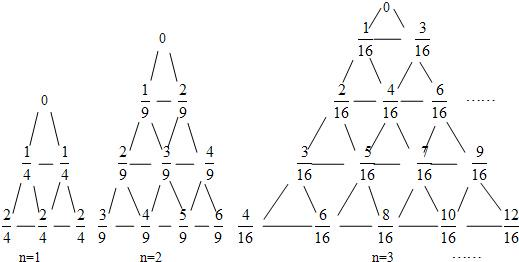
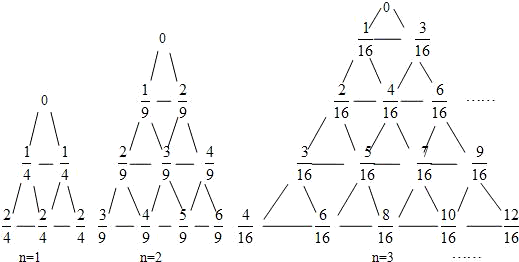
,前n项和为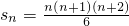 ,如下图所示,有一列三角形数表,其位于三角形的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列,依次记各三角形数表中的所有数之和为an,则
,如下图所示,有一列三角形数表,其位于三角形的三边及平行于某边的任一直线上的数(当数的个数不少于3时)都分别依次成等差数列,依次记各三角形数表中的所有数之和为an,则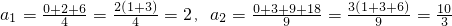 .
.
(1)求a3,a4,并写出an的表达式;
(2)令bn=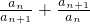 ,证明2n<b1+b2+b3+…+bn<2n+2(n∈N*).
,证明2n<b1+b2+b3+…+bn<2n+2(n∈N*).
解:(1)∵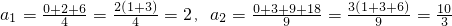 ,
,
∴a3= .
.
(2) ,
, ,
,
而 ,
,
∴2n<b1+b2+b3++bn<2n+2
分析:(1)由a1,a2可得a3= .
.
(2)由 ,知b1+b2+b3+…+bn=
,知b1+b2+b3+…+bn= ,由此知2n<b1+b2+b3++bn<2n+2.
,由此知2n<b1+b2+b3++bn<2n+2.
点评:本题考查数列的性质和应用及数列和不等式的综合运用,解题时要认真审题,仔细解答,注意合理地进行等价转化.
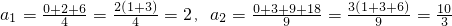 ,
,∴a3=
 .
.(2)
 ,
, ,
,而
 ,
,∴2n<b1+b2+b3++bn<2n+2
分析:(1)由a1,a2可得a3=
 .
.(2)由
 ,知b1+b2+b3+…+bn=
,知b1+b2+b3+…+bn= ,由此知2n<b1+b2+b3++bn<2n+2.
,由此知2n<b1+b2+b3++bn<2n+2.点评:本题考查数列的性质和应用及数列和不等式的综合运用,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
在古希腊,毕达哥拉斯学派把1,3,6,10,15,21,28,…这些数叫做三角形数,这是因为这些数目的点可以排成一个正三角形(如图).
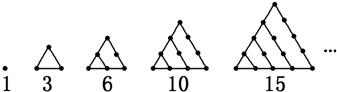
试问三角形数的一般表达式为( )

试问三角形数的一般表达式为( )
| A、n | ||
B、
| ||
| C、n2-1 | ||
D、
|
在古希腊,毕达哥拉斯学派把1,3,6,10,15,21,28,…这些数叫做三角形数,因为这些数对应的点可以排成一个正三角形,则第n个三角形数为( )


| A、n | ||
B、
| ||
| C、n2-1 | ||
D、
|