题目内容
 在四棱锥AB1中,AB1D1C平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
在四棱锥AB1中,AB1D1C平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.(1)求证:BD⊥平面PAC;
(2)若PA=AB,求PB与AC所成角的余弦值;
(3)若PA=
| 6 |
分析:(1)由四边形ABCD是菱形,知AC⊥BD,由PA⊥平面ABCD,知PA⊥BD,由此能够证明BD⊥平面PAC.
(2)过B作BM∥AC交DA延长线与M,连接PM,∠PBM或其补角为PB与AC所成角,由此能求出PB与AC所成角的余弦值.
(3)作BH⊥PC,连接HD,由PA⊥平面ABCD,知PB=PD,由CD=CB,PC=PC,知△PBC≌△PDC,由此能够证明PBC⊥面PDC.
(2)过B作BM∥AC交DA延长线与M,连接PM,∠PBM或其补角为PB与AC所成角,由此能求出PB与AC所成角的余弦值.
(3)作BH⊥PC,连接HD,由PA⊥平面ABCD,知PB=PD,由CD=CB,PC=PC,知△PBC≌△PDC,由此能够证明PBC⊥面PDC.
解答:(1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,
∵PA⊥平面ABCD,
∴PA⊥BD,
∵AC∩PA=A,
∴BD⊥平面PAC.
(2)解:过B作BM∥AC交DA延长线与M,
连接PM,∠PBM或其补角为PB与AC所成角,
∵BM∥AC,AM∥BC,
∴四边形MACB是平行四边形,
∴BM=AC=2
,
PB=PM=2
,
∴cos∠PBM=
.
(3)证明:作BH⊥PC,连接HD,
∵PA⊥平面ABCD,
∴PB=PD,
∵CD=CB,PC=PC,
∴△PBC≌△PDC,
∵BH⊥PC,∴HD⊥PC,
∴∠BHD为二面角的平面角,
∵AP=
,PB=
,PC=3
,BC=2,
∴BH=
,
cos∠BHD=0,
∴面PBC⊥面PDC.
∴AC⊥BD,
∵PA⊥平面ABCD,
∴PA⊥BD,
∵AC∩PA=A,
∴BD⊥平面PAC.
(2)解:过B作BM∥AC交DA延长线与M,
连接PM,∠PBM或其补角为PB与AC所成角,
∵BM∥AC,AM∥BC,
∴四边形MACB是平行四边形,
∴BM=AC=2
| 3 |
PB=PM=2
| 2 |
∴cos∠PBM=
| ||
| 4 |
(3)证明:作BH⊥PC,连接HD,
∵PA⊥平面ABCD,
∴PB=PD,
∵CD=CB,PC=PC,
∴△PBC≌△PDC,
∵BH⊥PC,∴HD⊥PC,
∴∠BHD为二面角的平面角,
∵AP=
| 6 |
| 10 |
| 2 |
∴BH=
| 2 |
cos∠BHD=0,
∴面PBC⊥面PDC.
点评:本题考查直线与平面垂直的证明,考查直线与平面所成角的余弦值的求法,考查平面与平面垂直的证明.解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
相关题目
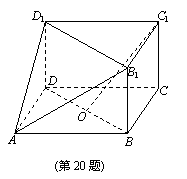
 (2012•河北区一模)如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=
(2012•河北区一模)如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB= ,AD=3,BB1=1.
,AD=3,BB1=1.
 ,AD=3,BB1=1.
,AD=3,BB1=1.
 ,AD=3,BB1=1.
,AD=3,BB1=1.