ЬтФПФкШн
дкЯТСагЩе§Ъ§ХХГЩЕФЪ§БэжаЃЌУПааЩЯЕФЪ§ДгзѓЕНгвЖМГЩЕШБШЪ§СаЃЌВЂЧвЫљгаЙЋБШЖМЕШгкqЃЌУПСаЩЯЕФЪ§ДгЩЯЕНЯТЖМГЩЕШВюЪ§СаЃЎ![]() БэЪОЮЛгкЕк
БэЪОЮЛгкЕк![]() ааЕк
ааЕк![]() СаЕФЪ§ЃЌЦфжа
СаЕФЪ§ЃЌЦфжа![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
|
|
|
|
|
| Ё |
| Ё |
|
|
|
|
|
| Ё |
| Ё |
|
|
|
|
|
| Ё |
| Ё |
|
|
|
|
|
| Ё |
| Ё |
| Ё | Ё | Ё | Ё | Ё | Ё | Ё | Ё |
|
|
|
|
|
| Ё |
| Ё |
| Ё | Ё | Ё | Ё | Ё | Ё | Ё | Ё |
ЃЈЂёЃЉ Чѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈЂђЃЉ Чѓ![]() ЕФМЦЫуЙЋЪНЃЛ
ЕФМЦЫуЙЋЪНЃЛ
ЃЈЂѓЃЉЩшЪ§СаЃћbnЃ§Тњзуbn=annЃЌЃћbnЃ§ЕФЧА![]() ЯюКЭЮЊ
ЯюКЭЮЊ![]() ЃЌЪдБШНЯ
ЃЌЪдБШНЯ![]() гыTn=
гыTn=![]() ( nЁЪN*) ЕФДѓаЁЃЌВЂЫЕУїРэгЩ.
( nЁЪN*) ЕФДѓаЁЃЌВЂЫЕУїРэгЩ.
НтЃКЃЈЂёЃЉЩшЕк4СаЙЋВюЮЊ![]() ЃЌдђ
ЃЌдђ ЃЎ
ЃЎ
ЙЪ![]() ЃЌгкЪЧ
ЃЌгкЪЧ![]() ЃЎ
ЃЎ
гЩгк![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌЙЪ
ЃЌЙЪ![]() ЃЎ
ЃЎ
ЃЈЂђЃЉдкЕк4СажаЃЌ![]() ЃЎ
ЃЎ
гЩгкЕк![]() ааГЩЕШБШЪ§СаЃЌЧвЙЋБШ
ааГЩЕШБШЪ§СаЃЌЧвЙЋБШ![]() ЃЌ
ЃЌ
ЫљвдЃЌ ![]() ЃЎ
ЃЎ
ЃЈЂѓЃЉгЩЃЈЂђЃЉПЩжЊ![]() ЃЎМДbn=
ЃЎМДbn=![]() ЃЎ
ЃЎ
Ыљвд![]()
![]() .
.
МД![]() ЃЌ
ЃЌ
ЙЪ![]() ЃЎ
ЃЎ
СНЪНЯрМѕЃЌЕУ![]()
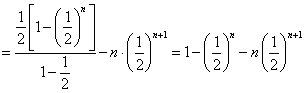 ЃЌ
ЃЌ
Ыљвд![]() ЃЎ
ЃЎ
Щшf(x)=2-![]() -
-![]() ( x >0)ЃЌ
( x >0)ЃЌ
МДf(x)=2-![]() -
-![]() =2-
=2-![]() =2-(2+ x)2-x.
=2-(2+ x)2-x.
вђЮЊf Ёф(x)= -[2-x+(2+ x)2-x(-1)ln2]= 2-x[(2+ x)ln2-1]
=2-x[ln22+ x - lne]=2-xln![]() ЃЌ
ЃЌ
ЧвЕБx>0ЪБЃЌx+2>2. Ыљвд22+ x>22= 4.
гкЪЧ![]() >
>![]() >1.
>1.
Ыљвдln![]() >0.
>0.
гж2-x>0ЃЌ
Ыљвддк(0ЃЌ+Ёо)ЩЯf Ёф(x) =2-xln![]() >0.
>0.
вђДЫКЏЪ§f(x)=2-![]() -
-![]() дк(0ЃЌ+Ёо)ЕЅЕїЕнді.
дк(0ЃЌ+Ёо)ЕЅЕїЕнді.
Ыљвд![]() ( nЁЪN*)ЪЧЕндіЪ§Са.
( nЁЪN*)ЪЧЕндіЪ§Са.
ЭЌРэЩшg(x)=![]() ( x >0)ЃЌ
( x >0)ЃЌ
вђЮЊgЁф(x)=![]() ?
?![]() = -
= -![]() <0 ( x >0)ЃЌ
<0 ( x >0)ЃЌ
ЙЪg(x)=![]() дк(0ЃЌ+Ёо)ЕЅЕїЕнМѕ.
дк(0ЃЌ+Ёо)ЕЅЕїЕнМѕ.
ЫљвдTn=![]() ( nЁЪN*)ЪЧЕнМѕЪ§Са.
( nЁЪN*)ЪЧЕнМѕЪ§Са.
ШнвзМЦЫуS1=f(1)=![]() ЃЌS2=f(2)=1ЃЌS3=f(3)=1
ЃЌS2=f(2)=1ЃЌS3=f(3)=1![]() ЃЌS4=f(4)=1
ЃЌS4=f(4)=1![]() ЃЌ
ЃЌ
T1= g(1)=1![]() ЃЌT2= g(2)=1
ЃЌT2= g(2)=1![]() ЃЌT3= g(3)=1
ЃЌT3= g(3)=1![]() ЃЌT4= g(4)=1
ЃЌT4= g(4)=1![]() ЃЌ
ЃЌ
ЯдШЛS1< T1ЃЌS2< T2ЃЌS3< T3ЃЌS4> T4ЃЌ
ЫљвдЕБnЁм3ЪБЃЌ![]() <TnЃЛЕБn>3ЪБЃЌ
<TnЃЛЕБn>3ЪБЃЌ![]() >Tn.
>Tn.

дкЯТСагЩе§Ъ§ХХГЩЕФЪ§БэжаЃЌУПааЩЯЕФЪ§ДгзѓЕНгвЖМГЩЕШБШЪ§СаЃЌВЂЧвЫљгаЙЋБШЖМЕШгк![]() ЃЌУПСаЩЯЕФЪ§ДгЩЯЕНЯТЖМГЩЕШВюЪ§СаЃЎ
ЃЌУПСаЩЯЕФЪ§ДгЩЯЕНЯТЖМГЩЕШВюЪ§СаЃЎ![]() БэЪОЮЛгкЕк
БэЪОЮЛгкЕк![]() ааЕк
ааЕк![]() СаЕФЪ§ЃЌЦфжа
СаЕФЪ§ЃЌЦфжа![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
|
|
|
|
|
| Ё |
| Ё |
|
|
|
|
|
| Ё |
| Ё |
|
|
|
|
|
| Ё |
| Ё |
|
|
|
|
|
| Ё |
| Ё |
| Ё | Ё | Ё | Ё | Ё | Ё | Ё | Ё |
|
|
|
|
|
| Ё |
| Ё |
| Ё | Ё | Ё | Ё | Ё | Ё | Ё | Ё |
ЃЈЂёЃЉ Чѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈЂђЃЉ Чѓ![]() ЕФМЦЫуЙЋЪНЃЛ
ЕФМЦЫуЙЋЪНЃЛ
ЃЈЂѓЃЉЩшЪ§СаЃћbnЃ§Тњзуbn=annЃЌЃћbnЃ§ЕФЧА![]() ЯюКЭЮЊ
ЯюКЭЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() .
.
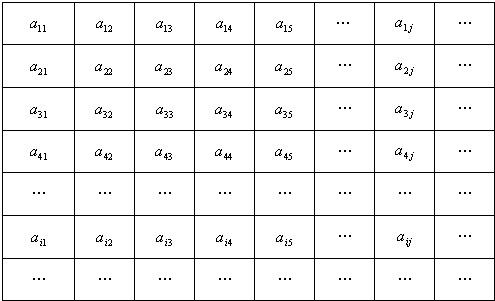
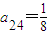 ЃЌa42=1ЃЌ
ЃЌa42=1ЃЌ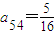 ЃЎ
ЃЎ
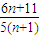 ЃЈ nЁЪN*ЃЉЕФДѓаЁЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ nЁЪN*ЃЉЕФДѓаЁЃЌВЂЫЕУїРэгЩЃЎ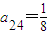 ЃЌa42=1ЃЌ
ЃЌa42=1ЃЌ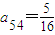 ЃЎ
ЃЎ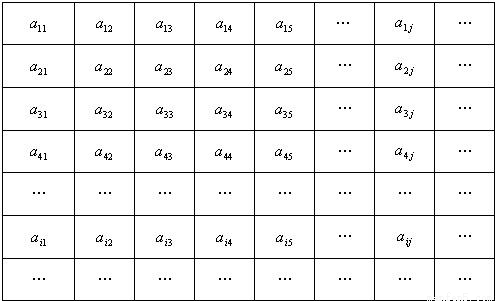
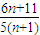 ЃЈ nЁЪN*ЃЉЕФДѓаЁЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ nЁЪN*ЃЉЕФДѓаЁЃЌВЂЫЕУїРэгЩЃЎ