Question

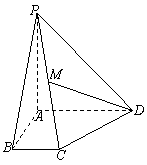
（本小题满分12分）如图，在四棱锥中，PA⊥底面ABCD，∥，∠=90°，，是的中点.

（1）求证：⊥；

（2）求平面与平面所成的锐二面角的余弦值；

（3）试探究线段上是否存在一点，使得∥面?若存在，确定点的位置；若不存在，请说明理由．

Answer 1

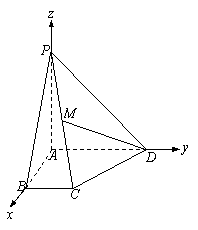
解：（1）不妨令BC＝1，以A为坐标原点，建立如图所示的空间直角坐标系．

则A（0，0，0），B（2，0，0），C（2，1，0），D（0，2，0），P（0，0，2）

所以M（1，，1），，.

因为,  所以.  ……………………………4分

（2）设平面PCD的法向量为＝(x，y，z),

由    .                     ……………6分

而平面PAB的法向量为,

∴cos＜,＞=.

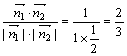∴所求二面角的余弦值为. …………………………………………………………8分

（3）假设线段PB上存在一点Q，有,