Question

已知二次函数f（x）的顶点坐标为（1，1），且f（0）=3，
（1）求函数f（x）的解析式；
（2）令g（x）=f（|x|）-m，（m∈R），若函数g（x）有四个零点，求实数m的取值范围．

Answer 1

分析：（1）设出二次函数f（x）的解析式，用待定系数法求出f（x）的解析式；
（2）画出函数y=m与y=f（|x|）的图象，图象有四个交点时，函数g（x）有四个零点，从而求出m的取值范围．

解答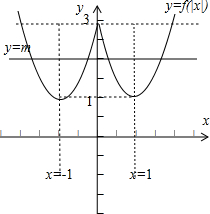：解：（1）∵二次函数f（x）的顶点坐标为（1，1），且f（0）=3，
设f（x）=a（x-1）²+1，
∴f（0）=a+1=3，解得a=2，
∴f（x）=2（x-1）²+1=2x²-4x+3；
（2）∵g（x）=f（|x|）-m，
设y=f（|x|），则y=2（|x|-1）²+1=

2(x-1)2+1，x≥0 2(x+1)2+1，x＜0

，
画出函数图象，如图；
由图象知，当1＜m＜3时，函数y=m与y=f（|x|）的图象有四个交点，
∴g（x）有四个零点，
∴m的取值范围是{m|1＜m＜3}．

点评：本题考查了求函数的解析式以及判定函数零点的问题，是基础题．