题目内容
如果存在实数x，使cosα=
+
成立，那么实数x的取值范围是（ ）
| x |
| 2 |
| 1 |
| 2x |
| A、{-1，1} |
| B、{x|x＜0或x=1} |
| C、{x|x＞0或x=-1} |
| D、{x|x≤-1或x≥1} |
分析：根据cosa∈[-1，1]得到
+
的范围限制，再求得x的范围即可．
| x |
| 2 |
| 1 |
| 2x |
解答：解：∵cosa∈[-1，1]
∴-1≤
+
≤1
即：
∴
∴x=1，-1
故选A
∴-1≤
| x |
| 2 |
| 1 |
| 2x |
即：
|
|
∴x=1，-1
故选A
点评：本题考查余弦函数的有界性，双边不等式的解法．
练习册系列答案
53随堂测系列答案
相关题目
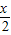
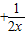成立，那么实数x的集合是（ ）
成立，那么实数x的取值范围是（ ）
成立，那么实数x的取值范围是（ ）