题目内容

已知数列{an}满足a1=1,an=a1+2a2+3a3+…+(n-1)an-1(n≥2),则数列{an}的通项an=_____________.

解析：由已知当n≥2时，an=a1+2a2+3a3+…+(n-1)an-1.               ①

可得an+1=a1+2a2+3a3+…+nan.                                                ②

由②-①,得an+1=(n+1)an.

由a1=1,得a2=a1=1,故当n≥2时，=n+1,即an=a1···…·=1·1·3

·…·n=,

即an=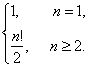

答案：an=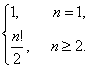


练习册系列答案
相关题目
已知数列{an}满足：a1=1且an+1=
3+4an
12-4an
， n∈N*．
（1）若数列{bn}满足：bn=
1
an-
1
2
(n∈N*)，试证明数列bn-1是等比数列；
（2）求数列{anbn}的前n项和Sn；
（3）数列{an-bn}是否存在最大项，如果存在求出，若不存在说明理由．
已知数列{an}满足
1
2
a1+
1
22
a2+
1
23
a3+…+
1
2n
an=2n+1则{an}的通项公式
 
．
已知数列{an}满足：a1=
3
2
，且an=
3nan-1
2an-1+n-1
（n≥2，n∈N*）．
（1）求数列{an}的通项公式；
（2）证明：对于一切正整数n，不等式a1•a2•…an＜2•n！
已知数列{an}满足an+1=|an-1|（n∈N*）
（1）若a1=
54
，求an；
（2）若a1=a∈（k，k+1），（k∈N*），求{an}的前3k项的和S3k（用k，a表示）
（2012•北京模拟）已知数列{an}满足an+1=an+2，且a1=1，那么它的通项公式an等于
2n-1
2n-1
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网