题目内容
12.设f(x)是定义在R上的奇函数,f′(x)为其导函数,且f(3)=0,当x>0时,有$\frac{xf′(x)-f(x)}{{x}^{2}}$<0恒成立,则不等式xf(x)>0的解集是(-3,0)∪(0,3).分析 利用函数的导数,判断函数的单调性,结合函数的奇偶性直接利用数形结合求解即可.
解答 解:设g(x)=$\frac{f(x)}{x}$,当x>0时,有g′(x)=$\frac{xf'(x)-f(x)}{x^2}<0$成立,可得g(x)=$\frac{f(x)}{x}$,在x>0时是减函数,
∵函数f(x)是定义在R上的奇函数,f(3)=0,
∴g(x)是偶函数,且g(-3)=g(3)=0.
则当x>0时,不等式xf(x)>0等价为x2•$\frac{f(x)}{x}$>0,即x2•g(x)>0,即g(x)>0,
则当x<0时,不等式xf(x)>0等价为x2•$\frac{f(x)}{x}$>0,即x2•g(x)>0,即g(x)>0,
作出g(x)对应的草图如图: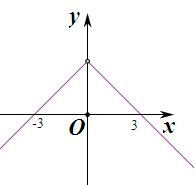
则不等式g(x)>0的解集是:(-3,3).
当x=0时,不等式xf(x)>0不成立,
故不等式xf(x)>0的解集是:(-3,0)∪(0,3).
故答案为:(-3,0)∪(0,3).
点评 本题考查不等式的求解,以及函数的导数的应用,根据条件构造函数,利用导数研究函数 单调性,以及利用数形结合的思想与方法是解决本题的关键.

练习册系列答案
相关题目
1.若(a+b+c)(b+c-a)=3bc且sinA=2sinBcosC,则△ABC是( )
| A. | 直角三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
 是等差数列,公差
是等差数列,公差 ,
, ,
,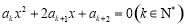 .
. 取不同正整数时,方程都有公共根;
取不同正整数时,方程都有公共根; ,
, ,
,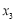 ,…,
,…, ,求证:
,求证: ,
, ,
, ,…,
,…, ,…是等差数列.
,…是等差数列.