题目内容
正三棱锥 内接于球
内接于球 ,且底面边长为
,且底面边长为 ,侧棱长为2,则球
,侧棱长为2,则球 的表面积为( )
的表面积为( )
A. |
B. |
C. |
D. |
C
解析如图,
设三棱锥 的外接球球心为O,半径为r,BC=CD=BD=
的外接球球心为O,半径为r,BC=CD=BD= ,AB=AC=AD=2,
,AB=AC=AD=2, ,M为正
,M为正 的中心,则DM=1,AM=
的中心,则DM=1,AM= ,OA=OD=r,所以
,OA=OD=r,所以 ,解得
,解得 ,所以
,所以 ,选C.
,选C.

练习册系列答案
相关题目
已知正方体外接球的体积是 ,那么正方体的棱长等于( )
,那么正方体的棱长等于( )
A. | B. | C. | D. |
某几何体的三视图如图所示,则该几何体的体积为( )
A. | B. | C. | D. |
一个正方体的体积是8,则这个正方体的内切球的表面积是( )
| A.8π |
| B.6π |
| C.4π |
| D.π |
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几体的体积为( )
| A.6 |
| B.9 |
| C.12 |
| D.18 |
一个几何体的三视图如图所示,则该几何体的体积是
| A.112 | B.80 | C.72 | D.64 |
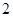 的正方形,俯视图是一个直径为
的正方形,俯视图是一个直径为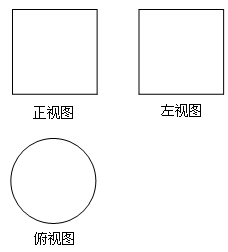

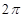
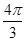
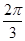
 ,球面上
,球面上 两点都在北纬45°圈上,它们的球面距离为
两点都在北纬45°圈上,它们的球面距离为 ,
, 点在东经30°上,则
点在东经30°上,则






