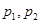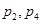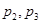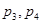题目内容
虚数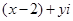 中
中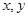 均为实数,当此虚数的模为1时,
均为实数,当此虚数的模为1时,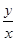 的取值范围是( )
的取值范围是( )
A.[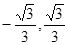 ] ] | B.[-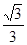 ,0)∪(0, ,0)∪(0,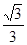 ] ] |
C.[-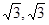 ] ] | D.[-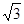 ,0)∪(0, ,0)∪(0,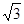 ] ] |
B
解析试题分析: ,即
,即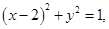 而
而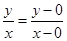 ,所以
,所以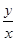 可以看成圆上的点和原点连线的斜率,设
可以看成圆上的点和原点连线的斜率,设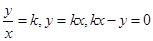 ,当直线与圆相切时,
,当直线与圆相切时,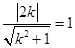 ,解得
,解得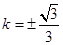 ,又因为
,又因为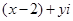 是虚数,所以
是虚数,所以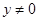 ,
,
所以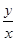 的取值范围是[-
的取值范围是[-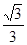 ,0)∪(0,
,0)∪(0,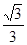 ].
].
考点:本小题主要考查复数的几何意义、两点间斜率公式、直线与圆的位置关系等,考查了学生转化问题的能力和数形结合思想的应用.
点评:将所求转化为圆上的点与原点连线的斜率是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知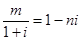 ,其中
,其中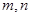 是实数,
是实数,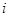 是虚数单位,则
是虚数单位,则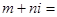 ( )
( )
A.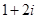 | B.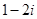 | C.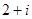 | D.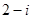 |
复数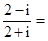
A.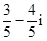 | B.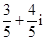 | C.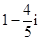 | D.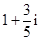 |
若复数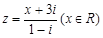 是实数,则
是实数,则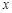 的值为
的值为
A.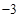 | B.3 | C.0 | D.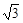 |
复数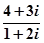 的共轭复数的虚部为( )
的共轭复数的虚部为( )
A.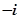 | B.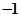 | C.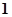 | D.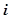 |
在复平面上,复数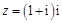 的共轭复数的对应点所在的象限是( )
的共轭复数的对应点所在的象限是( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
复数的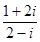 的共轭复数是
的共轭复数是
A.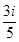 | B.—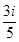 | C.i | D.—i |
已知 为虚数单位,则
为虚数单位,则 在复平面内对应的点位于
在复平面内对应的点位于
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
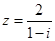 的四个命题,其中真命题为 ( )
的四个命题,其中真命题为 ( ) 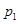 :
: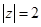 ,
, 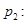

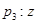 的共轭复数为
的共轭复数为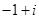
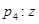 的虚部为
的虚部为