题目内容
9.已知函数f(x)=-x2+|x-a|.(a∈R)(1)当a=1时,求函数最大值.
(2)当a>0时,讨论函数单调性.
分析 (1)当x≥1时,f(x)=-x2+x-1,当x<1时,f(x)=-x2-x+1.利用单调性分别求出f(x)在每一段上的最大值取较大者即为答案.
(2)分别讨论f(x)在每段上单调性即可
解答 解:(1)①当x≥1时,f(x)=-x2+x-1,对称轴为x=$\frac{1}{2}$,
∴f(x)在[1,+∞)上为减函数,
fmax(x)=f(1)=-1.
②当x<1时,f(x)=-x2-x+1,对称轴为x=-$\frac{1}{2}$,
∴f(x)在(-∞,-$\frac{1}{2}$)上为增函数,在[-$\frac{1}{2}$,1)上为减函数,
∴fmax(x)=f(-$\frac{1}{2}$)=$\frac{5}{4}$.
综上所述:当a=1时,函数f(x)最大值为$\frac{5}{4}$.
(2))①当x≥a时,f(x)=-x2+x-a,对称轴为x=$\frac{1}{2}$,
(i)当a≥$\frac{1}{2}$时,f(x)在[a,+∞)上为减函数;
(ii)当0<a<$\frac{1}{2}$时,f(x)在[a,$\frac{1}{2}$]上为增函数,在($\frac{1}{2}$,+∞)上为减函数.
②当x<a时,f(x)=-x2-x+a,对称轴为x=-$\frac{1}{2}$,
∴f(x)在(-∞,-$\frac{1}{2}$]上为增函数,在(-$\frac{1}{2}$,a)上为减函数.
综上所述:a≥$\frac{1}{2}$时,f(x)在(-∞,-$\frac{1}{2}$]上为增函数,在(-$\frac{1}{2}$,+∞)上为减函数;
0<a<$\frac{1}{2}$时,f(x)在(-∞,-$\frac{1}{2}$]上为增函数,在(-$\frac{1}{2}$,a)上为减函数,在[a,$\frac{1}{2}$]上为增函数,在($\frac{1}{2}$,+∞)上为减函数.
点评 本题考查了二次函数的单调性,要注意区间与对称轴的关系.

 金钥匙试卷系列答案
金钥匙试卷系列答案| A. | ab>0,bc>0 | B. | ab>0,bc<0 | C. | ab<0,bc>0 | D. | ab<0,bc<0 |
 已知函数f(x)=x|x-m|,x∈R,且f(4)=0.
已知函数f(x)=x|x-m|,x∈R,且f(4)=0.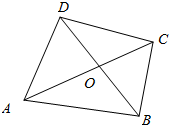 如图所示,在四边形ABCD中,$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$,对角线AC与BD交于点O,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,用$\overrightarrow{a}$和$\overrightarrow{b}$表示$\overrightarrow{AB}$和$\overrightarrow{AD}$.
如图所示,在四边形ABCD中,$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$,对角线AC与BD交于点O,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,用$\overrightarrow{a}$和$\overrightarrow{b}$表示$\overrightarrow{AB}$和$\overrightarrow{AD}$.