题目内容
已知点集L{(x,y)|y=| m |
| n |
| m |
| n |
(1)求数列{an},{bn}的通项公式;
(2)求
| OPn |
| OPn+1 |
(3)设Cn=
| ||
n•an•|
|
分析:(1)由y=
•
,
=(2x-2b, 1),
=(1, 1+2b),得:y=2x+1,由此入手结合题意能够导出an=n-1(n∈N*),bn=2n-1(n∈N*).
(2)由Pn(n-1,2n-1),知Pn+1(n,2n+1),由此能够导出当n=1时,
•
有最小值3.
(3)由当n≥2时,Pn(n-1,2n-1),得:Cn=
=
=
-
,由此能够求出C2+C3+…+Cn的值.
| m |
| n |
| m |
| n |
(2)由Pn(n-1,2n-1),知Pn+1(n,2n+1),由此能够导出当n=1时,
| OPn |
| OPn+1 |
(3)由当n≥2时,Pn(n-1,2n-1),得:Cn=
| ||
n•an•|
|
| 1 |
| n(n-1) |
| 1 |
| n-1 |
| 1 |
| n |
解答:解:(1)由y=
•
,
=(2x-2b, 1),
=(1, 1+2b),
得:y=2x+1
即L:y=2x+1
∵P1为L的轨迹与y轴的交点,
∴P1(0,1)则a1=0,b1=1
∵数列{an}为等差数列,且公差为1,
∴an=n-1(n∈N*),
代入y=2x+1,得:bn=2n-1(n∈N*)
(2)∵Pn(n-1,2n-1),
∴Pn+1(n,2n+1),
∴
•
=(n-1,2n-1)•(n,2n+1)=5n2-n-1=5(n-
)2-
∵n∈N*,所以当n=1时,
•
有最小值,为3.
(3)当n≥2时,Pn(n-1,2n-1),
得:an•|
|=
(n-1),
Cn=
=
=
-
,
∴C2+C3++Cn=(1-
)+(
-
)++(
-
)=1-
.
| m |
| n |
| m |
| n |
得:y=2x+1
即L:y=2x+1
∵P1为L的轨迹与y轴的交点,
∴P1(0,1)则a1=0,b1=1
∵数列{an}为等差数列,且公差为1,
∴an=n-1(n∈N*),
代入y=2x+1,得:bn=2n-1(n∈N*)
(2)∵Pn(n-1,2n-1),
∴Pn+1(n,2n+1),
∴
| OPn |
| OPn+1 |
| 1 |
| 10 |
| 21 |
| 20 |
∵n∈N*,所以当n=1时,
| OPn |
| OPn+1 |
(3)当n≥2时,Pn(n-1,2n-1),
得:an•|
| PnPn+1 |
| 5 |
Cn=
| ||
n•an•|
|
| 1 |
| n(n-1) |
| 1 |
| n-1 |
| 1 |
| n |
∴C2+C3++Cn=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| n |
点评:本题考查数列性质的综合运用,具有一定的难度,解题时要注意挖掘隐含条件.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
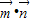 },其中
},其中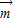 =(2x-2b,1),
=(2x-2b,1),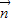 =(1,1+2b)为向量,点列Pn(an,bn)在点集L中,P1为L的轨迹与y轴的交点,已知数列{an}为等差数列,且公差为1,3.
=(1,1+2b)为向量,点列Pn(an,bn)在点集L中,P1为L的轨迹与y轴的交点,已知数列{an}为等差数列,且公差为1,3.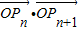 的最小值;(其中O为坐标原点)
的最小值;(其中O为坐标原点) (n≥2),求:C2+C3+…+Cn的值.
(n≥2),求:C2+C3+…+Cn的值.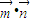 },其中
},其中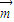 =(2x-b,1),
=(2x-b,1),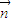 =(1,b+1),点列Pn(an,bn)(n∈N+)在L中,p1为L与y轴的交点,数列{an}是公差为1的等差数列.
=(1,b+1),点列Pn(an,bn)(n∈N+)在L中,p1为L与y轴的交点,数列{an}是公差为1的等差数列. ,令Sn=f(1)+f(2)+f(3)+…+f(n),试写出Sn关于n的表达式;
,令Sn=f(1)+f(2)+f(3)+…+f(n),试写出Sn关于n的表达式; ,给定奇数m(m为常数,m∈N+,m>2).是否存在k∈N+,,使得
,给定奇数m(m为常数,m∈N+,m>2).是否存在k∈N+,,使得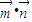 },其中
},其中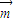 =(2x-2b,1),
=(2x-2b,1),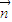 =(1,1+2b)为向量,点列Pn(an,bn)在点集L中,P1为L的轨迹与y轴的交点,已知数列{an}为等差数列,且公差为1,3.
=(1,1+2b)为向量,点列Pn(an,bn)在点集L中,P1为L的轨迹与y轴的交点,已知数列{an}为等差数列,且公差为1,3.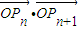 的最小值;(其中O为坐标原点)
的最小值;(其中O为坐标原点)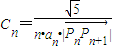 (n≥2),求:C2+C3+…+Cn的值.
(n≥2),求:C2+C3+…+Cn的值.