题目内容

数列{a_n}，已知a₁=3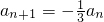， $数学公式$ ，则a_n的通项公式为________．

$\text{[math]}$
分析：通过数列的递推关系式，判断数列是等比数列，求出通项公式即可．
解答：因为数列{a_n}，已知a₁=3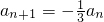， $\text{[math]}$ ，所以数列是等比数列，公比为- $\text{[math]}$ ，
所以a_n=a₁q^n-1= $\text{[math]}$ ．
故答案为： $\text{[math]}$ ．
点评：本题是基础题，考查数列的基本运算，考查数列的判断，通项公式的解法．

练习册系列答案

孟建平中考错题本系列答案

轻松过关优选卷系列答案

走向名校小升初考前集训系列答案

智慧课堂同步讲练测系列答案

名师指导延边大学出版社系列答案

新课标同步课堂优化课堂系列答案

五步三查导学案系列答案

爱尚课好学生课时检测系列答案

七彩题卡口算应用一点通系列答案

课堂导学案湖南教育出版社系列答案

相关题目

数列{a_n}，已知对任意正整数n，a₁+a₂+a₃+…+a_n=2ⁿ-1，则a₁²+a₂²+a₃²+…+a_n² 等于（　　）

A、（2ⁿ-1）²

6、数列{a_n}，已知a₁=1，当n≥2时a_n=a_n-1+2n-1，依次计算a₂、a₃、a₄后，猜想a_n的表达式是（　　）

某医院近30天每天因患甲型H1N1流感而入院就诊的人数依次构成数列{a_n}，已知a₁=1，a₂=2，且满足a_n+2-a_n=1+（-1）ⁿ（n∈N*），则该医院30天内因患甲型H1N1流感而入院就诊的人数共有（　　）

数列{an}中,已知对任意n∈N*,a1+a2+a3+…+an=3n-1,则+++…+等于(　　)

(A)(3n-1)2 (B) (9n-1)

(C)9n-1 (D) (3n-1)

在数列{an}中,已知a1=2,a2=7,an+2等于anan+1(n∈N*)的个位数,则a2013的值是(　　)

(A)8 (B)6 (C)4 (D)2