题目内容
已知数列{an}的前n项和为Sn,点(n,Sn)在抛物线y=x2上,数列{bn}满足b1=a1,点(bn,bn+1)在直线y=3x上,
(Ⅰ)分别求{an},{bn}的通项公式;
(Ⅱ)求数列{an·bn}的前n项和Tn。
(Ⅰ)分别求{an},{bn}的通项公式;
(Ⅱ)求数列{an·bn}的前n项和Tn。
解:(Ⅰ)对于数列{an}有Sn=n2,
当n=1时,有a1-S1=1,
当n≥2时,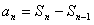 =n2-(n-1)2=2n-1,
=n2-(n-1)2=2n-1,
n=1也符合上式,
故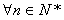 都有an=2n-1;
都有an=2n-1;
对于数列{bn}有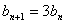 ,
,
故{bn}是以b1=a1=1为首项,以3为公比的等比数列,
所以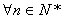 都有
都有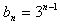 。
。
(Ⅱ)由(Ⅰ)知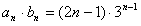 ,
,
从而Tn=a1b1+a2b2+…+anbn
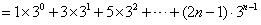 ,
,
于是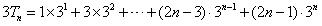 ,
,
错位相减并整理得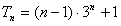 。
。
当n=1时,有a1-S1=1,
当n≥2时,
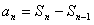 =n2-(n-1)2=2n-1,
=n2-(n-1)2=2n-1,n=1也符合上式,
故
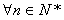 都有an=2n-1;
都有an=2n-1;对于数列{bn}有
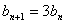 ,
,故{bn}是以b1=a1=1为首项,以3为公比的等比数列,
所以
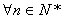 都有
都有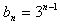 。
。(Ⅱ)由(Ⅰ)知
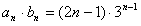 ,
,从而Tn=a1b1+a2b2+…+anbn
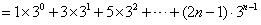 ,
,于是
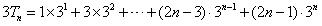 ,
,错位相减并整理得
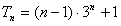 。
。
练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |