题目内容
对于函数f(x),若在其定义域内存在两个实数a,b(a<b),使当x∈[a,b]时,f(x)的值域也是[a,b],则称函数f(x)为“科比函数”.若函数f(x)=k+
是“科比函数”,则实数k的取值范围 ( )
| x+2 |
分析:根据题意可得到:
,即方程k+
=x有两个不相等的实数根,分别画出左右两边函数:y=
和y=x-k的图象,结合图象法可得答案.
|
| x+2 |
| x+2 |
解答: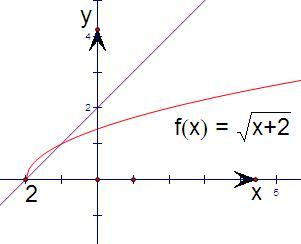 解:∵函数f(x)=k+
解:∵函数f(x)=k+
是“科比函数”,且是增函数,
∴
此式表明:方程k+
=x有两个不相等的实数根,
即方程
=x-k有两个不相等的实数根,
分别画出左右两边函数:y=
和y=x-k的图象,
当直线y=x-k与曲线y=
相切时,
=x-k有唯一解,解得k=-
;
当直线y=x-k与曲线上的点(-2,0)时,
解得k=-2;
结合图象可得:当两个函数的图象有两个不同的交点时,
实数k的取值范围是(-
,-2].
故选B.
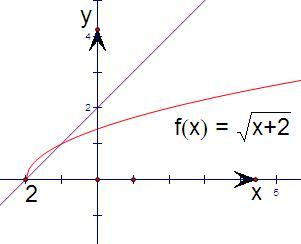 解:∵函数f(x)=k+
解:∵函数f(x)=k+| x+2 |
∴
|
此式表明:方程k+
| x+2 |
即方程
| x+2 |
分别画出左右两边函数:y=
| x+2 |
当直线y=x-k与曲线y=
| x+2 |
| x+2 |
| 9 |
| 4 |
当直线y=x-k与曲线上的点(-2,0)时,
解得k=-2;
结合图象可得:当两个函数的图象有两个不同的交点时,
实数k的取值范围是(-
| 9 |
| 4 |
故选B.
点评:本题主要考查了函数的值域,以及函数的单调性,同时考查了数形结合的数学思想和分析问题的能力,属于中档题.

练习册系列答案
相关题目