题目内容
复数z=x+yi(x,y∈R)满足|z-1|=x,则复数z对应的点Z(x,y)的轨迹方程为
y2=2x-1(x≥0)
y2=2x-1(x≥0)
.分析:由z=x+yi(x,y∈R),可得z-1=x-1+yi(x,y∈R),|z-1|=x,利用复数模的概念即可求得复数z对应的点Z(x,y)的轨迹方程.
解答:解:∵z=x+yi(x,y∈R),|z-1|=x,
∴
=x(x≥0),
两边平方得:y2=2x-1(x≥0),
∴复数z对应的点Z(x,y)的轨迹方程为:y2=2x-1(x≥0),
故答案为:y2=2x-1(x≥0).
∴
| (x-1)2+y2 |
两边平方得:y2=2x-1(x≥0),
∴复数z对应的点Z(x,y)的轨迹方程为:y2=2x-1(x≥0),
故答案为:y2=2x-1(x≥0).
点评:本题考查复数求模,关键在于将|z-1|=x转化为关于x,y的关系式,着重考查复数模的运算,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
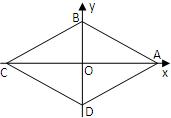 已知菱形ABCD四个顶点对应的复数分别为4,2i,-4,-2i.
已知菱形ABCD四个顶点对应的复数分别为4,2i,-4,-2i.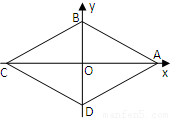
 |=2y
|=2y |≥2
|≥2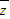 |=2y
|=2y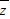 |≥2
|≥2 |=2y
|=2y |≥2
|≥2