题目内容
(2013•朝阳区一模)已知命题p:?x∈R,x2+x-1>0;命题q:?x∈R,sinx+cosx=
.则下列判断正确的是( )
| 2 |
分析:利用配方法求得x2+x-1的范围,说明命题p为假命题,利用三角函数的化积求得sinx+cosx的最大值等于1,说明命题q为真命题,然后利用符合命题的真值表加以判断即可得到答案.
解答:解:由x2+x-1=(x+
)2-
≥-
,所以命题p:?x∈R,x2+x-1>0为假命题;
由sinx+cosx=
sin(x+
),当x=
时sinx+cosx=
.
所以命题q:?x∈R,sinx+cosx=
是真命题.
由以上可知:¬p是真命题;q是真命题;pⅤq是真命题;(¬p)∧q是真命题.
故选D.
| 1 |
| 2 |
| 5 |
| 4 |
| 5 |
| 4 |
由sinx+cosx=
| 2 |
| π |
| 4 |
| π |
| 4 |
| 2 |
所以命题q:?x∈R,sinx+cosx=
| 2 |
由以上可知:¬p是真命题;q是真命题;pⅤq是真命题;(¬p)∧q是真命题.
故选D.
点评:本题考查了复合命题的真假,考查了配方法求函数的值域,解答的关键是熟记复合命题的真值表,是基础题.
复合命题的真值表:
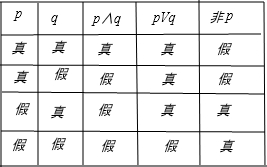
复合命题的真值表:


练习册系列答案
相关题目
