Question

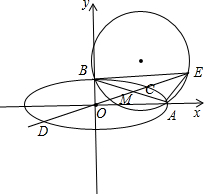
已知A，B是焦距为4

2

的椭圆E：

x2

a2

+

y2

b2

=1(a＞b＞0)的右顶点和上顶点，过原点O与线段AB中点M的直线交椭圆于C，D两点（点C在第一象限内），直线OM的方程为y=

1

3

x
（1）求椭圆的方程；
（2）延长OC到E，使

OE

=

2

OC

，求△ABE的外接圆方程．

Answer 1

分析：（1）由于A（a，0），B（0，b），利用中点坐标公式可得：线段AB的中点M(

a

2

，

b

2

)．由于直线OM的方程为y=

1

3

x，可得a与b的关系．又焦距2c=4

2

，与a²=b²+c²联立即可得出；
（2）由（1）可得M(

3

2

，

1

2

)，设E（x，y），利用

OE

=

2

OC

，可得E的坐标．设△ABE的外接圆的方程为
x²+y²+Dx+Ey+F=0，把A，B，E三点的坐标代入即可得出D，E，F．

解答：解：（1）∵A（a，0），B（0，b），∴线段AB的中点M(

a

2

，

b

2

)．
∵直线OM的方程为y=

1

3

x，∴

b

2

=

1

3

×

a

2

，即a=3b．
又焦距2c=4

2

，联立

a=3b 2c=4 2 a2=b2+c2

解得c=2

2

，b=1，a=3．
∴椭圆E的方程为

x2

9

+y2=1．
（2）联立

y= 1 3 x x2 9 +y2=1

解得C(

3 2

2

，

2

2

)．
设E（x，y），∵

OE

=

2

OC

，
∴（x，y）=

2

(

3 2

2

，

2

2

)=（3，1），即E（3，1）．
设△ABE的外接圆的方程为x²+y²+Dx+Ey+F=0
把A，B，E三点的坐标代入可得

1+E+F=0 9+3D+F=0 9+1+3D+E+F=0

，解得

D=-3 E=-1 F=0

．
∴．△ABE的外接圆的方程为x²+y²-3x-y=0．

点评：本题考查了椭圆的标准方程及其性质、中点坐标公式、向量的运算、利用“待定系数法”求三角形外接圆的方程等基础知识与基本技能方法，属于难题．