题目内容
已知函数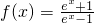 .
.
(Ⅰ)求f(x)的反函数f-1(x);
(Ⅱ)讨论f(x)的奇偶性.
解:(Ⅰ)由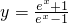 ,得yex-y=ex+1,
,得yex-y=ex+1,
从而yex-ex=y+1,(y-1)ex=y+1,∴ .
.
由 ,得y<-1,或y>1.
,得y<-1,或y>1.
再由 ,得
,得 ,
,
∴ (x<-1或x>1).
(x<-1或x>1).
(Ⅱ)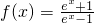 中,∵ex-1≠0,∴x≠0.∴函数f(x)的定义域为{x|x≠0},它关于原点对称.
中,∵ex-1≠0,∴x≠0.∴函数f(x)的定义域为{x|x≠0},它关于原点对称.
∵ =
= ,
,
∴函数f(x)是奇函数.
分析:(Ⅰ)由给出的函数解析式求出函数的值域,再由解析式解出x,即把x用含有y的代数式表示,最后把x和y互换即可;
(Ⅱ)函数的定义域关于原点对称,然后直接利用判断函数奇偶性的定义,换x为-x整理即可.
点评:本题考查了函数反函数的求法,考查了函数奇偶性的判断,求一个函数的反函数,一定不要忘记注函数的定义域,即原函数的值域,判断函数的奇偶性,前提是定义域关于原点对称,此题是中档题.
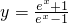 ,得yex-y=ex+1,
,得yex-y=ex+1,从而yex-ex=y+1,(y-1)ex=y+1,∴
 .
.由
 ,得y<-1,或y>1.
,得y<-1,或y>1.再由
 ,得
,得 ,
,∴
 (x<-1或x>1).
(x<-1或x>1).(Ⅱ)
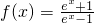 中,∵ex-1≠0,∴x≠0.∴函数f(x)的定义域为{x|x≠0},它关于原点对称.
中,∵ex-1≠0,∴x≠0.∴函数f(x)的定义域为{x|x≠0},它关于原点对称.∵
 =
= ,
,∴函数f(x)是奇函数.
分析:(Ⅰ)由给出的函数解析式求出函数的值域,再由解析式解出x,即把x用含有y的代数式表示,最后把x和y互换即可;
(Ⅱ)函数的定义域关于原点对称,然后直接利用判断函数奇偶性的定义,换x为-x整理即可.
点评:本题考查了函数反函数的求法,考查了函数奇偶性的判断,求一个函数的反函数,一定不要忘记注函数的定义域,即原函数的值域,判断函数的奇偶性,前提是定义域关于原点对称,此题是中档题.

练习册系列答案
相关题目
 .
. .
. 个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.
个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值. .
. 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围. .
. 成等差数列,且
成等差数列,且 =9,求a的值.
=9,求a的值. .
.