题目内容
13.已知实数a,b,c满足a+b=2c,则直线l:ax-by+c=0恒过定点(-$\frac{1}{2}$,$\frac{1}{2}$),该直线被圆x2+y2=9所截得弦长的取值范围为[$\sqrt{34}$,6].
分析 由条件a+b=2c,直线l:ax-by+c=0,即-2ax+2by=2c,可得直线l:ax-by+c=0恒过定点,过定点(-$\frac{1}{2}$,$\frac{1}{2}$)的最长弦为圆的直径6,最短弦与此直径垂直.
解答 解:由条件a+b=2c,直线l:ax-by+c=0,即-2ax+2by=2c,
所以点(-$\frac{1}{2}$,$\frac{1}{2}$)在直线-2ax+2by=2c上,故直线l:ax-by+c=0过定点(-$\frac{1}{2}$,$\frac{1}{2}$);
过定点(-$\frac{1}{2}$,$\frac{1}{2}$)的最长弦为圆的直径6,最短弦与此直径垂直,由于定点与圆心的距离为$\frac{\sqrt{2}}{2}$,
所以最短弦长为2$\sqrt{9-\frac{1}{2}}$=$\sqrt{34}$,
所以直线被圆x2+y2=9所截得弦长的取值范围为[$\sqrt{34}$,6].
故答案为:(-$\frac{1}{2}$,$\frac{1}{2}$),[$\sqrt{34}$,6].
点评 本题主要考查经过定点的直线,考查直线被圆x2+y2=9所截得弦长的取值范围,属于中档题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
3.设数列{an}的前n项和为Sn,若an+Sn=1,则a4=( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{32}$ | D. | $\frac{1}{64}$ |
4.已知集合A={x|x2-2x>0},B={x|log2(x+1)<1},则A∩B等于( )
| A. | (-∞,0) | B. | (2,+∞) | C. | (0,1) | D. | (-1,0) |
8.设m,n是两条不同的直线,α,β是两个不同的平面,下列命题正确的是( )
| A. | m⊥α,n⊥β,且α⊥β,则m⊥n | B. | m∥α,n∥β,且α∥β,则m∥n | ||
| C. | m⊥α,n?β,m⊥n,则α⊥β | D. | m?α,n?α,m∥β,n∥β,则α∥β |
18.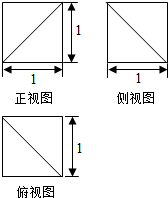 某几何体的三视图如图所示,则该几何体的体积是( )
某几何体的三视图如图所示,则该几何体的体积是( )
 某几何体的三视图如图所示,则该几何体的体积是( )
某几何体的三视图如图所示,则该几何体的体积是( )| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
5.已知点O为双曲线C的对称中心,过点O的两条直线l1与l2的夹角为60°,直线l1与双曲线C相交于点A1,B1,直线l2与双曲线C相交于点A2,B2,若使|A1B1|=|A2B2|成立的直线l1与l2有且只有一对,则双曲线C离心率的取值范围是( )
| A. | ($\frac{2\sqrt{3}}{3}$,2] | B. | [$\frac{2\sqrt{3}}{3}$,2) | C. | ($\frac{2\sqrt{3}}{3}$,+∞) | D. | [$\frac{2\sqrt{3}}{3}$,+∞) |