Question

（本小题满分12分）已知函数。

（1）若曲线在处的切线的方向向量为，且函数在时有极值，求的单调区间；

（2）在（1）的条件下，若函数在上与有两个不同的交点，若在区间上的最小值，求实数的值。

Answer 1

(1)∵¦(x)=x3+ax2+bx+5

∴¦’(x)=3x2+2ax+b…………………………………………………1分

由已知¦(x)在x=1处的切线斜率为=3

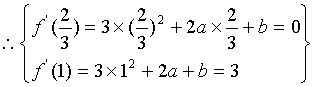
∴ a=2, b=-4 ………………………………………………………4分

∴¦(x)=x3+2x2-4X+5, ¦‘(x)=3x2+4x-4

令¦(x)>0 得 x<-2 或x >

令¦‘(x)<0 得 -2< x <

∴¦(x)在(-∞,-2),( ,+∞)上分别是增函数，¦(x)在(-2, )上是减函数 ……………………………………………………………………6分

（2）由（1）可知，y=f(x)在x=-2时取得极大值，f(-2)=13

且f(-3)=8,f(-1)=4

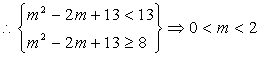 …………………………………8分

又g(x)=x2-2mx+1=(x-m)2+1-m2

当0<m<1时，g(x)在[1,2]上的最小值为

g(1)=2-2m=-,∴m=与0<m<1矛盾……………………………10分

②当1≤m<2时，g(x)在[1,2]最小值为

g(m)=1-m2=-

∴m=或m=-（舍去）

综上可知，m= ……………………………………………12分