题目内容
设函数f(x)＝mx2－mx－1．
(1)若对于一切实数x，f(x)＜0恒成立，求m的取值范围；
(2)对于xÎ[1，3]，f(x)＞－m＋x－1恒成立，求m的取值范围．
解答：(1)要mx2－mx－1＜0对任意实数x恒成立，
若m＝0，显然－1＜0成立； ………………………………2分
若m≠0，则
解得－4＜m＜0． ………………………………4分
所以－4＜m≤0． ………………………………6分
(2)因为x2－x＋1＞0对一切实数恒成立，所以f(x)＞－m＋x－1Þm(x2－x＋1)＞x．
所以m＞
在xÎ[1，3]上恒成立． ……………………8分
因为函数y＝＝
在xÎ[1，3]上的最大值为1，…………………10分
所以只需m＞1即可．所以m的取值范围是{m|m＞1}． …………………12分
练习册系列答案
相关题目
x＋2m和圆x2＋y2＝n2相切，其中m，n∈N*，0＜| m－n |≤1，若函数f (x)＝mx+1－n的零点x0∈（k，k＋1），k∈Z，则k＝
x＋2m和圆x2＋y2＝n2相切，其中m，n∈N*，0＜| m－n |≤1，若函数f (x)＝mx+1－n的零点x0∈（k，k＋1），k∈Z，则k＝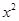
－mx－1.