题目内容
已知数列{an}满足an+1=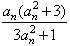 ,
,
(Ⅰ)若方程f(x)=x的解称为函数y=f(x)的不动点,求an+1=f(an)的不动点的值;
(Ⅱ)若a1=2,bn=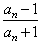 ,求证:数列{lnbn}是等比数列,并求数列{bn}的通项;
,求证:数列{lnbn}是等比数列,并求数列{bn}的通项;
(Ⅲ)当任意n∈N*时,求证:b1+b2+b3+…+bn<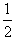 。
。
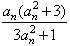 ,
,(Ⅰ)若方程f(x)=x的解称为函数y=f(x)的不动点,求an+1=f(an)的不动点的值;
(Ⅱ)若a1=2,bn=
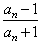 ,求证:数列{lnbn}是等比数列,并求数列{bn}的通项;
,求证:数列{lnbn}是等比数列,并求数列{bn}的通项;(Ⅲ)当任意n∈N*时,求证:b1+b2+b3+…+bn<
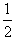 。
。 解:(Ⅰ)由方程an+1=f(an)得an=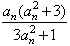 ,
,
解得an=0,或an=-1,或an=1;
(Ⅱ)∵an+1+1=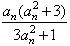 +1=
+1=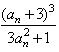 ,
,
an+1-1=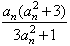 -1=
-1=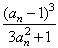 ,
,
∴两式相除得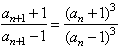 ,即bn+1=bn3,
,即bn+1=bn3,
由a1=2可以得到bn>0,
则lnbn+1=3lnbn,
又b1=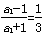 ,
,
得lnb1=-ln3,
∴数列{lnbn}是以-ln3为首项,3为公比的等比数列,
∴lnbn=(-ln3)·3n-1=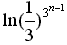 ,
,
从而bn=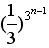 (n∈N*)。
(n∈N*)。
(Ⅲ)证明:任意n∈N*,3n-1≥n,
∴bn=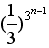 ≤
≤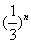 ,
,
从而b1+b2+b3+…+bn<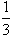 +(
+(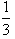 )2+(
)2+(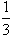 )3+…+(
)3+…+(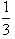 )n
)n
=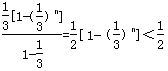 。
。
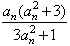 ,
,解得an=0,或an=-1,或an=1;
(Ⅱ)∵an+1+1=
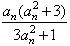 +1=
+1=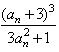 ,
,an+1-1=
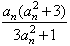 -1=
-1=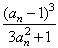 ,
,∴两式相除得
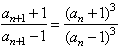 ,即bn+1=bn3,
,即bn+1=bn3,由a1=2可以得到bn>0,
则lnbn+1=3lnbn,
又b1=
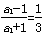 ,
,得lnb1=-ln3,
∴数列{lnbn}是以-ln3为首项,3为公比的等比数列,
∴lnbn=(-ln3)·3n-1=
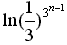 ,
,从而bn=
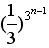 (n∈N*)。
(n∈N*)。(Ⅲ)证明:任意n∈N*,3n-1≥n,
∴bn=
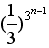 ≤
≤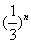 ,
,从而b1+b2+b3+…+bn<
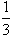 +(
+(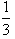 )2+(
)2+(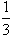 )3+…+(
)3+…+(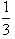 )n
)n=
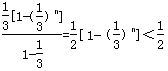 。
。
练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目