题目内容
【题目】求由直线x=1、x=2、y=0及曲线![]() 围成的图形的面积S.
围成的图形的面积S.
【答案】详见解析
【解析】(1)分割:
在区间[1,2]上等间隔地插入n-1个点,将它等分成n个小区间:
![]() ,则第i个区间为
,则第i个区间为![]() (i=1,2,…,n),其长度为Δx=
(i=1,2,…,n),其长度为Δx=![]() ,
,
分别过上述n-1个分点作x轴的垂线,把曲边梯形分成n个小曲边梯形(如图),它们的面积记作:ΔS1,ΔS2,…,ΔSn,则小曲边梯形面积的和为S=![]() .
.

(2)近似代替:
记f(x)=![]() .当n很大,即Δx很小时,在区间
.当n很大,即Δx很小时,在区间![]() 上,可以认为f(x)=
上,可以认为f(x)=![]() 的值变化很小,近似地等于一个常数,不妨认为它等于
的值变化很小,近似地等于一个常数,不妨认为它等于 .从图形上看,就是用平行于x轴的直线段近似地代替小曲边梯形的曲边.这样,在区间
.从图形上看,就是用平行于x轴的直线段近似地代替小曲边梯形的曲边.这样,在区间![]() 上,用小矩形面积ΔSi′近似地代替ΔSi,即在局部小范围内“以直代曲”,则有ΔSi≈ΔSi′=
上,用小矩形面积ΔSi′近似地代替ΔSi,即在局部小范围内“以直代曲”,则有ΔSi≈ΔSi′= Δx=
Δx=![]() =
=![]() (i=1,2,…,n).
(i=1,2,…,n).
(3)求和:
小曲边梯形的面积和Sn=![]() Si≈
Si≈![]() Si′=
Si′=![]() =
=
![]()
=![]()
=![]()
![]() .从而得到S的近似值S≈Sn=
.从而得到S的近似值S≈Sn=![]() .
.
(4)取极限:
分别将区间[1,2]等分成8,16,20,…等份时,Sn越来越趋向于S,
从而有S=![]() Sn=
Sn=![]() .
.
∴由直线x=1,x=2,y=0及曲线y=![]() 围成的图形的面积S为
围成的图形的面积S为![]() .
.

【题目】某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表。
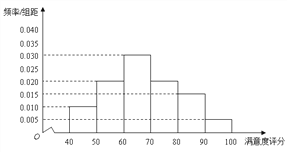
A地区用户满意度评分的频率分布直方图

B地区用户满意度评分的频数分布表
(Ⅰ)在答题卡上作出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);
(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
估计哪个地区的满意度等级为不满意的概率大?说明理由


