题目内容
如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.
(1)求证:△ABE≌△ACD;
(2)若AB=6,BC=4,求AE.

解:(1)在ΔABE和ΔACD中,∵AB=AC ∠ABE=∠ACD
又∠BAE=∠EDC ∵BD//MN ∴∠EDC=∠DCN,∵直线MN是圆的切线,∴∠DCN=∠CAD ∴∠BAE=∠CAD,∴ΔABE≌ΔACD(角、边、角)
(2)∵∠EBC=∠BCM ∠BCM=∠BDC,∴∠EBC=∠BDC=∠BAC BC=CD=4
又∠BEC=∠BAC+∠ABE=∠EBC+∠ABE=∠ABC=∠ACB ∴BC=BE=4
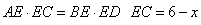 设AE=x,易证 ΔABE∽ΔDEC
设AE=x,易证 ΔABE∽ΔDEC
∴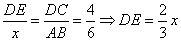
又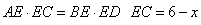
∴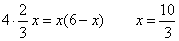
即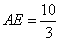

练习册系列答案
相关题目
 ,则AC=
,则AC=  的斜率为______________________。
的斜率为______________________。  ”的证明过程:
”的证明过程: ”应用了
”应用了 所表示的数是 ( )
所表示的数是 ( )
 个不同的球放入
个不同的球放入 个不同的盒中,每个盒内至少有
个不同的盒中,每个盒内至少有 个球,则不同的放法种数为 ( )
个球,则不同的放法种数为 ( ) B.36 C.48 D.96
B.36 C.48 D.96 的偶函数为 ( )
的偶函数为 ( ) B.
B.
 D.
D.
 B.
B. C.
C. D.
D.