题目内容
函数y=cos2x-2cosx的值域为
- A.[-1，1]
- B.[-1，3]
- C.[-
，3] - D.[-，-1]
C
分析：利用余弦函数的二倍角公式升幂将y=cos2x-2cosx转化为关于cosx的关系式，配方即可求其值域．
解答：∵y=cos2x-2cosx
=2cos2x-2cosx-1
=2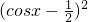
-．
∵-1≤cosx≤1，
∴当cosx=-1时，ymax=2
-=3，
当cosx=
时，ymin=-．
∴函数y=cos2x-2cosx的值域为[-，3]
故选C．
点评：本题考查二倍角的余弦，考查复合三角函数的单调性，考查配方法，属于中档题．
分析：利用余弦函数的二倍角公式升幂将y=cos2x-2cosx转化为关于cosx的关系式，配方即可求其值域．
解答：∵y=cos2x-2cosx
=2cos2x-2cosx-1
=2
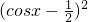-．∵-1≤cosx≤1，
∴当cosx=-1时，ymax=2
-=3，当cosx=
时，ymin=-．∴函数y=cos2x-2cosx的值域为[-
，3]故选C．
点评：本题考查二倍角的余弦，考查复合三角函数的单调性，考查配方法，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
为了得到函数y=sin（2x-
）的图象，可以将函数y=cos2x的图象（ ）
| π |
| 6 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|