题目内容
设f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2,若对任意的x∈[t,t+2],不等式f(x+t)≥2f(x)恒成立,则实数t的取值范围是( )A.
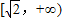
B.[2,+∞)
C.(0,2]
D.
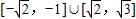
【答案】分析:2f(x)=f(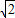 x),由题意可知f(x)为R上的增函数,故对任意的x∈[t,t+2],不等式f(x+t)≥2f(x)恒成立可转化为
x),由题意可知f(x)为R上的增函数,故对任意的x∈[t,t+2],不等式f(x+t)≥2f(x)恒成立可转化为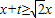 对任意的x∈[t,t+2]恒成立,此为一次不等式恒成立,解决即可.也可取那个特值排除法.
对任意的x∈[t,t+2]恒成立,此为一次不等式恒成立,解决即可.也可取那个特值排除法.
解答:解:(排除法)当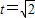 则
则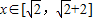 得
得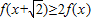 ,即
,即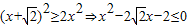 在
在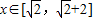 时恒成立,而
时恒成立,而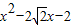 最大值,是当
最大值,是当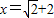 时出现,故
时出现,故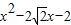 的最大值为0,则f(x+t)≥2f(x)恒成立,排除B项,
的最大值为0,则f(x+t)≥2f(x)恒成立,排除B项,
同理再验证t=3时,f(x+t)≥2f(x)恒成立,排除C项,t=-1时,f(x+t)≥2f(x)不成立,故排除D项
故选A
点评:本题考查函数单调性的应用:利用单调性处理不等式恒成立问题.将不等式化为f(a)≥f(b)形式是解题的关键.
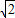 x),由题意可知f(x)为R上的增函数,故对任意的x∈[t,t+2],不等式f(x+t)≥2f(x)恒成立可转化为
x),由题意可知f(x)为R上的增函数,故对任意的x∈[t,t+2],不等式f(x+t)≥2f(x)恒成立可转化为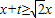 对任意的x∈[t,t+2]恒成立,此为一次不等式恒成立,解决即可.也可取那个特值排除法.
对任意的x∈[t,t+2]恒成立,此为一次不等式恒成立,解决即可.也可取那个特值排除法.解答:解:(排除法)当
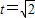 则
则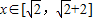 得
得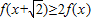 ,即
,即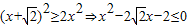 在
在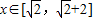 时恒成立,而
时恒成立,而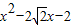 最大值,是当
最大值,是当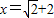 时出现,故
时出现,故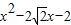 的最大值为0,则f(x+t)≥2f(x)恒成立,排除B项,
的最大值为0,则f(x+t)≥2f(x)恒成立,排除B项,同理再验证t=3时,f(x+t)≥2f(x)恒成立,排除C项,t=-1时,f(x+t)≥2f(x)不成立,故排除D项
故选A
点评:本题考查函数单调性的应用:利用单调性处理不等式恒成立问题.将不等式化为f(a)≥f(b)形式是解题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
设f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=-f(x).当x∈[0,2]时,f(x)=2x-x2+a(a是常数).则x∈[2,4]时的解析式为( )
| A、f(x)=-x2+6x-8 | B、f(x)=x2-10x+24 | C、f(x)=x2-6x+8 | D、f(x)=x2-6x+8+a |