题目内容
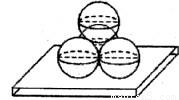
把四个半径都是1的球中的三个放在桌面上，使它两两外切，然后在它们上面放上第四个球，使它与前三个都相切，求第四个球的最高点与桌面的距离．
解：四个球心连线是正三棱锥．棱长均为2
∴ED=
，OD=
=
∴AO=
=
∴第四个球的最高点与桌面的距离为+2
即（OA加上两个半径）
分析：先求四个球心连线是正三棱锥的高，而第四个球的最高点与桌面的距离即为高加上两个半径，从而求出所求．
点评：本题主要考查了点到面的距离，同时考查了转化与划归的思想，以及计算能力，属于中档题．
∴ED=
，OD==∴AO=
=∴第四个球的最高点与桌面的距离为
+2即（OA加上两个半径）
分析：先求四个球心连线是正三棱锥的高，而第四个球的最高点与桌面的距离即为高加上两个半径，从而求出所求．
点评：本题主要考查了点到面的距离，同时考查了转化与划归的思想，以及计算能力，属于中档题．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
相关题目
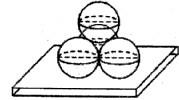如图，把四个半径都是1的球中的三个放在桌面上，使它两两外切，然后在它们上面放上第四个球，使它与前三个都相切，在这四个球之间有一个小球和这四个球都外切，则这个小球的半径是