Question

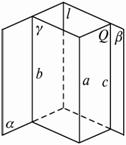
求证：如果一条直线和两个相交的平面都平行，那么这条直线和它们的交线平行．

已知：如图，a∩b=l，a∥a，a∥b．

求证：a∥l．

 

Answer 1

答案：
解析：

证明：过a作平面γ，交平面a于b，∵a∥a，∴a∥b． 同样，过a作平面δ交平面b于c， ∵a∥b，∴a∥c．∴b∥c． 又∵bb且cb，∴b∥b． 又平面a经过b交b于l， ∴b∥l．又a∥b，∴a∥l． 点评：应用线面平行的性质定理时，应着力寻找过已知直线的平面与已知平面的交线，有时为了得到交线还需作出辅助平面．