题目内容
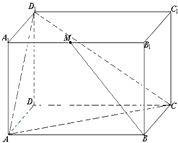 如图所示,已知长方体ABCD-A1B1C1D1中,AD=3,AB=AA1=4,M是A1B1的中点.
如图所示,已知长方体ABCD-A1B1C1D1中,AD=3,AB=AA1=4,M是A1B1的中点.
(1)求BM与平面ACD1所成的角;
(2)求点M到平面ACD1的距离.
解 (1)按如图所示建立空间直角坐标系,可得有关点的坐标为D(0,0,0)、A(3,0,0)、B(3,4,0),C(0,4,0),A1(3,0,4),B1(3,4,4),D1(0,0,4),M(3,2,4),进一步有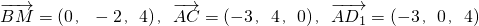 .
.
设平面ACD1的法向量为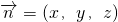 ,则
,则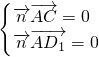 ,即
,即 .取z=3,得x=4,y=3.
.取z=3,得x=4,y=3.
所以平面ACD1的一个法向量为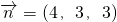 .
.
记 ,
,
于是,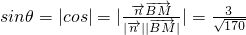 ,
, .
.
所以,直线BM与平面ACD1所成角为 .
.
(2)记点M到平面ACD1的距离为d.
由(1)知,平面ACD1的一个法向量为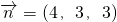 ,
, ,
,
于是,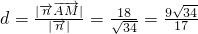 .
.
所以点M到平面ACD1的距离为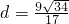 .
.
分析:(1)首先建立空间直角坐标系,写出相关点的坐标,再求出向量 的坐标和平面ACD1的法向量
的坐标和平面ACD1的法向量 ,最后求
,最后求 与
与 的夹角的余弦值,取绝对值后即为线面角的正弦值
的夹角的余弦值,取绝对值后即为线面角的正弦值
(2)由(1)知平面ACD1的法向量 ,再求向量
,再求向量 的坐标,最后求
的坐标,最后求 在
在 方向上的投影的长度即为M到平面ACD1的距离
方向上的投影的长度即为M到平面ACD1的距离
点评:本题考查了利用空间向量解决立体几何问题的方法和思路,解题时要学会熟练的求平面的法向量,并体会空间线面角、面面角是怎样转化为线线角的.
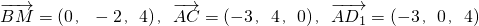 .
.设平面ACD1的法向量为
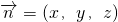 ,则
,则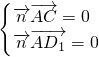 ,即
,即 .取z=3,得x=4,y=3.
.取z=3,得x=4,y=3.所以平面ACD1的一个法向量为
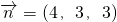 .
.记
 ,
,于是,
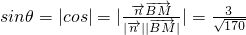 ,
, .
.所以,直线BM与平面ACD1所成角为
 .
.(2)记点M到平面ACD1的距离为d.
由(1)知,平面ACD1的一个法向量为
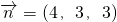 ,
, ,
,于是,
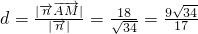 .
. 所以点M到平面ACD1的距离为
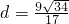 .
.分析:(1)首先建立空间直角坐标系,写出相关点的坐标,再求出向量
 的坐标和平面ACD1的法向量
的坐标和平面ACD1的法向量 ,最后求
,最后求 与
与 的夹角的余弦值,取绝对值后即为线面角的正弦值
的夹角的余弦值,取绝对值后即为线面角的正弦值(2)由(1)知平面ACD1的法向量
 ,再求向量
,再求向量 的坐标,最后求
的坐标,最后求 在
在 方向上的投影的长度即为M到平面ACD1的距离
方向上的投影的长度即为M到平面ACD1的距离点评:本题考查了利用空间向量解决立体几何问题的方法和思路,解题时要学会熟练的求平面的法向量,并体会空间线面角、面面角是怎样转化为线线角的.

练习册系列答案
相关题目
 (2006•静安区二模)如图所示,已知长方体ABCD-A1B1C1D1中,AC与BD交于E点,且AB=AD=2,两条异面直线A1D与AC所成的角的大小为
(2006•静安区二模)如图所示,已知长方体ABCD-A1B1C1D1中,AC与BD交于E点,且AB=AD=2,两条异面直线A1D与AC所成的角的大小为 (2009•黄浦区一模)如图所示,已知长方体ABCD-A1B1C1D1中,AD=3,AB=AA1=4,M是A1B1的中点.
(2009•黄浦区一模)如图所示,已知长方体ABCD-A1B1C1D1中,AD=3,AB=AA1=4,M是A1B1的中点. 如图所示,已知长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=4,E是棱CC1上的点,且CE=1.
如图所示,已知长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=4,E是棱CC1上的点,且CE=1. 如图所示,已知长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=4,E是棱CC1上的点,且BE⊥B1C.
如图所示,已知长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=4,E是棱CC1上的点,且BE⊥B1C. 中,
中,
 ,
, 是棱
是棱 上的点,且
上的点,且 。
。
 的长;
的长; 平面
平面 ;
; 与平面
与平面