题目内容
如图,已知三棱锥A-BCD的侧视图,俯视图都是直角三角形,尺寸如图所示.(1)求异面直线AB与CD所成角的余弦值;
(2)在线段AC上是否存在点F,使得BF⊥面ACD?若存在,求出CF的长度;若不存在说明理由.
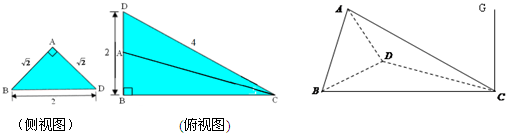
分析:(1)取BD的中点O,连AO,以O为原点建立空间直角坐标系,分别求出异面直线AB与CD的方向向量,代入向量夹角公式,即可得到异面直线AB与CD所成角的余弦值;
(2)设
=λ
,根据BF⊥面ACD,则BF⊥CA,BF⊥AD,我们分别求出BF,CA,AD对应向量的坐标,结合向量垂直数量积为0,可以构造关于λ的方程,解方程求出满足条件的λ值,进而即可求出CF的长度;
(2)设
| CF |
| CA |
解答: 解:(1)取BD的中点O,连AO,则AO⊥面CBD.
解:(1)取BD的中点O,连AO,则AO⊥面CBD.
以O为原点建立空间直角坐标系,如图.
A(0,0,1),B(1,0,0),C(1,2
,0),D(-1,0,0).
=(1,0,-1),
=(-2,-2
,0),cos<
,
>=-
.
所以所求异面直线AB与CD所成角的余弦值为
; (5分)
(2)设
=λ
,
则
=
+
=(-λ,2
(1-λ),λ)
由BF⊥面ACD得:
解得λ=
,
|
|=
|
|=
,(5分)
 解:(1)取BD的中点O,连AO,则AO⊥面CBD.
解:(1)取BD的中点O,连AO,则AO⊥面CBD.以O为原点建立空间直角坐标系,如图.
A(0,0,1),B(1,0,0),C(1,2
| 3 |
| AB |
| CD |
| 3 |
| AB |
| CD |
| ||
| 4 |
所以所求异面直线AB与CD所成角的余弦值为
| ||
| 4 |
(2)设
| CF |
| CA |
则
| BF |
| BC |
| CF |
| 3 |
由BF⊥面ACD得:
|
解得λ=
| 6 |
| 7 |
|
| CF |
| 6 |
| 7 |
| CA |
| 6 |
| 7 |
| 14 |
点评:本题考查的知识点是异面直线及其所成的角,直线与平面垂直的判定与性质,其中建立空间直角坐标系,将空间中直线与直线的夹角问题,直线与直线的垂直问题转化为向量问题是解答本题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
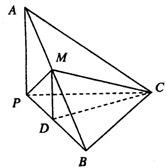 如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.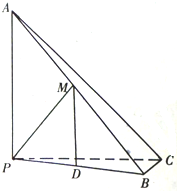 如图,已知三棱锥A-PBC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且AB=2MP.
如图,已知三棱锥A-PBC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且AB=2MP.
 如图,已知三棱锥A-BCD的棱长都相等,E,F分别是棱AB,CD的中点,则EF与BC所成的角是( )
如图,已知三棱锥A-BCD的棱长都相等,E,F分别是棱AB,CD的中点,则EF与BC所成的角是( ) 如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB的中点,D为PB的中点,且△PMB为正三角形.