题目内容
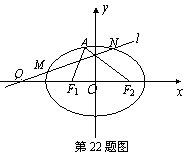
如图,已知椭圆C: ![]() 的左、右焦点分别为F1、F2,离心率为
的左、右焦点分别为F1、F2,离心率为![]() ,点A是椭圆上任一点,△AF1F2的周长为
,点A是椭圆上任一点,△AF1F2的周长为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点![]() 任作一动直线l交椭圆C于M,N两点,记
任作一动直线l交椭圆C于M,N两点,记![]() ,若在线段MN上取一点R,使得
,若在线段MN上取一点R,使得![]() ,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.
,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.
解(Ⅰ)∵△AF1F2的周长为![]() ,
,
∴![]() 即
即![]() . ……………………(1分)
. ……………………(1分)
又![]() 解得
解得![]() ………………(3分)
………………(3分)
∴椭圆C的方程为![]() ………………………………(4分)
………………………………(4分)
(Ⅱ)由题意知,直线l的斜率必存在,
设其方程为![]()
由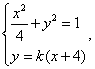
得![]() …………………………………(6分)
…………………………………(6分)
则![]() ……………………………………(7分)
……………………………………(7分)
由![]() ,得
,得![]()
∴![]() ∴
∴![]() .……………………………………(8分)
.……………………………………(8分)
设点R的坐标为(![]() ),由
),由![]() ,
,
得![]()
∴![]()
解得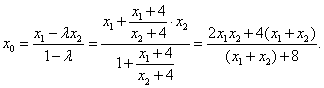 ………………(10分)
………………(10分)
而![]()
![]()
∴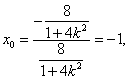 …………………………………………………(13分)
…………………………………………………(13分)
故点R在定直线![]() 上. ………………………………………………(14分)
上. ………………………………………………(14分)

练习册系列答案
相关题目
 如图,已知椭圆C:
如图,已知椭圆C: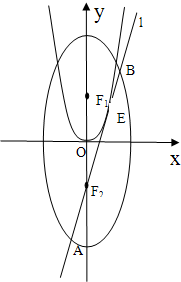 如图,已知椭圆
如图,已知椭圆 如图,已知椭圆C:
如图,已知椭圆C: 如图,已知椭圆
如图,已知椭圆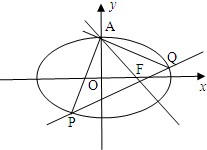 (2012•梅州一模)如图,已知椭圆C:
(2012•梅州一模)如图,已知椭圆C: