Question

【题目】已知△ABC的三个内角A，B，C所对的边分别为a，b，c，若三个内角A，B，C成等差数列，且a= ，b= ，求sinC的值．

Answer 1

【答案】解：∵三个内角A，B，C成等差数列，
∴2B=A+C，
∵A+B+C=π，
∴3B=π，即B= ，
∵a= ，b= ，
∴由正弦定理 得：sinA= = = ，
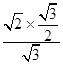∵a＜b，∴A＜B，即A= ，
则sinC=sin（A+B）=sinAcosB+cosAsinB= × + × =
【解析】由三内角成等差数列及内角和定理求出B的度数，再由a与b的值，利用正弦定理求出sinA的值，确定出A的度数，由sinC=sin（A+B），利用两角和与差的正弦函数公式化简，将A与B的度数代入计算即可求出值．
【考点精析】通过灵活运用正弦定理的定义和余弦定理的定义，掌握正弦定理:；余弦定理:;;即可以解答此题．