题目内容
如图,四棱锥P-ABCD中,PA⊥底面ABCD.四边形ABCD中,AB⊥AD,AB+AD=4,CD=![]() ,∠CDA=45°.
,∠CDA=45°.
(1)求证:平面PAB⊥平面PAD;
(2)设AB=AP.若直线PB与平面PCD所成的角为30°,求线段AB的长.(注意:BC与AD未必平行)
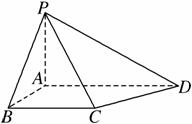
解析:(1)证明:因为PA⊥平面ABCD,
 AB⊂平面ABCD,
AB⊂平面ABCD,
所以PA⊥AB.
又AB⊥AD,PA∩AD=A,
所以AB⊥平面PAD.
又AB⊂平面PAB,所以平面PAB⊥平面PAD.。。。。。。。。(4分)
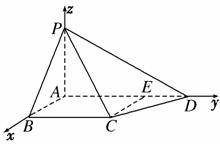
(2)以A为坐标原点,建立空间直角坐标系A-xyz(如图).
在平面ABCD内,作CE∥AB交AD于点E,则CE⊥AD.
在Rt△CDE中,DE=CD·cos45°=1,CE=CD·sin45°=1.
设AB=AP=t,则B(t,0,0),P(0,0,t).
由AB+AD=4得AD=4-t,
所以E(0,3-t,0),C(1,3-t,0),D(0,4-t,0),![]() =(-1,1,0),
=(-1,1,0),
![]() =(0,4-t,-t).
=(0,4-t,-t).
设平面PCD的一个法向量为n=(x,y,z),
由n⊥![]() ,n⊥
,n⊥![]() ,得
,得![]()
取x=t,得平面PCD的一个法向量n=(t,t,4-t).。。。。。。。。。。。(8分)
又![]() =(t,0,-t),故由直线PB与平面PCD所成的角为30°得
=(t,0,-t),故由直线PB与平面PCD所成的角为30°得
cos60°=|![]() |,即
|,即![]() =
=![]() ,
,
解得t=![]() 或t=4(舍去,因为AD=4-t>0),所以AB=
或t=4(舍去,因为AD=4-t>0),所以AB=![]() ..。。。。。。。。。。。(12分)
..。。。。。。。。。。。(12分)

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,CE∥AB.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,CE∥AB. 如图,四棱锥P-ABCD的底面ABCD是正方形,AC∩BD=O,PA⊥底面ABCD,OE⊥PC于E.
如图,四棱锥P-ABCD的底面ABCD是正方形,AC∩BD=O,PA⊥底面ABCD,OE⊥PC于E. 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥平面ABCD,点E,F分别是AB和PC的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥平面ABCD,点E,F分别是AB和PC的中点.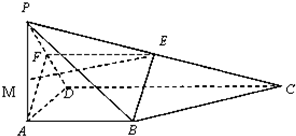 如图,四棱锥P-ABCD,PA⊥底面ABCD,AB∥CD,AB⊥AD,AB=AD=
如图,四棱锥P-ABCD,PA⊥底面ABCD,AB∥CD,AB⊥AD,AB=AD=