题目内容
关于下列命题:①函数y=tanx在第一象限是增函数;
②函数y=cos2(
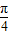 -x)是偶函数;
-x)是偶函数;③函数y=4sin(2x-
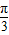 )的一个对称中心是(
)的一个对称中心是(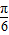 ,0);
,0);④函数y=sin(x+
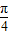 )在闭区间[
)在闭区间[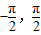 ]上是增函数.
]上是增函数.写出所有正确的命题的题号: .
【答案】分析:利用正切函数单调性判断①的正误;利用余弦函数的奇偶性判断②的正误;把对称中心坐标代入方程,是否处理确定③的正误;利用函数的单调性判断④的正误.
解答:解:①函数y=tanx在第一象限是增函数;显然不正确,正切函数在类似[0,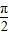 )上是增函数,第一象限是增函数,错误.
)上是增函数,第一象限是增函数,错误.
②函数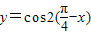 =sin2x是偶函数,是错误的;
=sin2x是偶函数,是错误的;
③因为x=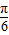 时,函数
时,函数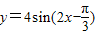 =0,所以函数
=0,所以函数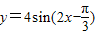 的一个对称中心是(
的一个对称中心是(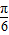 ,0);正确.
,0);正确.
④函数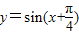 在闭区间
在闭区间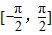 上是增函数.这是不正确的.在
上是增函数.这是不正确的.在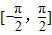 上函数有增有减.
上函数有增有减.
故答案为:③
点评:本题是基础题,考查三角函数的基本性质,包括:对称性、奇偶性、单调性、对称中心的知识,明确基本函数的基本性质,是解题的关键,所以平时学习注意基本知识的掌握和巩固.
解答:解:①函数y=tanx在第一象限是增函数;显然不正确,正切函数在类似[0,
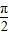 )上是增函数,第一象限是增函数,错误.
)上是增函数,第一象限是增函数,错误.②函数
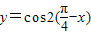 =sin2x是偶函数,是错误的;
=sin2x是偶函数,是错误的;③因为x=
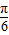 时,函数
时,函数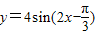 =0,所以函数
=0,所以函数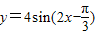 的一个对称中心是(
的一个对称中心是(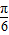 ,0);正确.
,0);正确.④函数
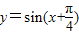 在闭区间
在闭区间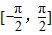 上是增函数.这是不正确的.在
上是增函数.这是不正确的.在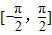 上函数有增有减.
上函数有增有减.故答案为:③
点评:本题是基础题,考查三角函数的基本性质,包括:对称性、奇偶性、单调性、对称中心的知识,明确基本函数的基本性质,是解题的关键,所以平时学习注意基本知识的掌握和巩固.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在第一象限是增函数;
在第一象限是增函数;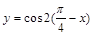 是奇函数;
是奇函数; 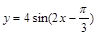 的一个对称中心是(
的一个对称中心是(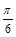 ,0);
,0);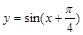 在闭区间
在闭区间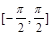 上是增函数.
上是增函数. 在第一象限是增函数;②函数
在第一象限是增函数;②函数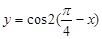 是偶函数;
是偶函数; 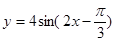 的一个对称中心是(
的一个对称中心是(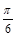 ,0);
,0); 在闭区间
在闭区间 上是增函数;
上是增函数;