Question

19．如图，ABCD为空间四边形，点E、F分别是AB、BC的中点，点G、H分别在CD、AD上，且DH=$\frac{1}{3}$AD，DG=$\frac{1}{3}$CD，求证：直线EH、FG必相交于一点，且这个交点在直线BD上．

Answer 1

分析 连接EF，HG，由已知条件推导出G，E，F，H四点共面，再由EF与GH不能平行，能证明直线EH、FG必相交于一点，且这个交点在直线BD上．

解答 证明：连接EF，HG，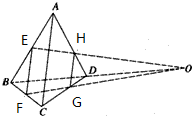
∵点E、F分别是AB、BC的中点，
∴EF∥AC，
又∵点G、H分别在CD、AD上，且DH=$\frac{1}{3}$AD，DG=$\frac{1}{3}$CD，
∴HG∥AC，
∴EF∥HG，
故G，E，F，H四点共面
又∵EF与GH不能平行，
∴EF与GH相交，设交点为O，
则O∈面ABD，O∈面BCD，而平面ABD∩平面BCD=BD，
∴EF，GH，BD交于一点．
∴直线EH、FG必相交于一点，且这个交点在直线BD上．

点评 本题考查直线EH、FG必相交于一点，且这个交点在直线BD上的证明，是基础题，解题时要认真审题，注意空间思维能力的培养．