Question

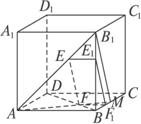
正方体ABCD—A₁B₁C₁D₁的棱长为a,E在AB₁上,F在BD上,且B₁E=BF.

求证:EF∥平面BC₁.

Answer 1

证法一:如图,连结AF并延长交BC或其延长线于M,连结B₁M,则△AFD∽△MFB,

∴AF∶FM=DF∶FB.

又AB₁=BD,B₁E=BF,∴DF=AE.

故DF∶FB=AE∶EB₁,∴AF∶FM=AE∶EB₁.故EF∥B₁M.

又B₁M平面BC₁,EF在平面BC₁外,因此EF∥平面BC₁.

证法二:分别作FF₁∥DC,EE₁∥AB,交BC于F₁,交BB₁于E₁,连结E₁F₁.

∵FF₁∶DC=BF∶BD,EE₁∶AB=B₁E∶B₁A,

又∵AB=CD,BD=B₁A,BF=B₁E,

∴FF₁=EE₁.∴EE₁∥FF₁且EE₁=FF₁.

∴EE₁F₁F为平行四边形.∴EF∥E₁F₁.

又∵E₁F₁平面BC₁,EF在平面BC₁外,∴EF∥平面BC₁.