题目内容
运货卡车以每小时x千米的匀速行驶130千米,按交通法规限制50≤x≤100(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油(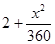 )升,司机的工资是每小时14元.
)升,司机的工资是每小时14元.
(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
【答案】
(Ⅰ)
 ;(Ⅱ)
;(Ⅱ) km/h时,最低费用的值为
km/h时,最低费用的值为 .
.
【解析】
试题分析:(Ⅰ)行车总费用包括两部分:一部分是油耗;另一部分是司机工资,首先表示出行车时间为 ,故司机工资为
,故司机工资为 (元),耗油为
(元),耗油为 (元),故行车总费用为二部分的和;(Ⅱ)
(元),故行车总费用为二部分的和;(Ⅱ)
 ,由基本不等式
,由基本不等式 可求最小值,注意等号成立的条件(
可求最小值,注意等号成立的条件( 时取等号),如果等号取不到,可考虑利用对号函数
时取等号),如果等号取不到,可考虑利用对号函数
 的图象,通过单调性求最值.
的图象,通过单调性求最值.
试题解析:(Ⅰ)设所用时间为 ,
, .
.
所以,这次行车总费用y关于x的表达式是
(或 ,
, )
)
(Ⅱ)
仅当 ,即
,即 时,上述不等式中等号成立
时,上述不等式中等号成立
答:当 km/h时,这次行车的总费用最低,最低费用的值为26
km/h时,这次行车的总费用最低,最低费用的值为26 元
元
考点:1、函数的解析式;2、基本不等式.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目