Question

（本小题满分12分）

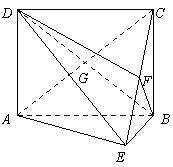如图，矩形中，，，为上的点，且，．

（Ⅰ）求证：平面；

（Ⅱ）求证：平面；

（Ⅲ）求三棱锥的体积．

Answer 1

（Ⅰ）证明：平面，．∴平面，则．…… (2分)

又平面，则．∴平面．                 …… (4分)

（Ⅱ）证明：依题意可知：是中点．平面，则，而．

∴是中点．                                                       ………(6分)

      在中，，∴平面．                             ………(8分)

（Ⅲ）解法一：平面，∴，而平面．

        ∴平面，∴平面．                               ………(９分)

        是中点，∴是中点．∴且．

        平面，∴．                                     ……(10分)

        ∴中，．∴．       ……(11分)

    ∴．                                   ……(12分)

解法二：．       ……(12分) u