题目内容
下列命题中,真命题的个数有( )
①?x∈R,x2-x+
≥0;
②?x>0,lnx+
≤2;
③”a>b”是“ac2>bc2”的充要条件;
④y=2x-2-x是奇函数.
①?x∈R,x2-x+
| 1 |
| 4 |
②?x>0,lnx+
| 1 |
| lnx |
③”a>b”是“ac2>bc2”的充要条件;
④y=2x-2-x是奇函数.
分析:①由配方可判断出其真假;②取x∈(0,1),即可知命题的真假;③取c=0即可否定③;④利用奇函数的定义可判断出是否是奇函数.
解答:解:①∵?x∈R,x2-x+
=(x-
)2≥0,∴①是真命题.
②当0<x<1时,lnx<0,∴?x>0,lnx+
<0≤2,∴②是真命题.
③当c=0时,由a>b⇒ac2=bc2=0;而由ac2>bc2⇒a>b,故“a>b”是“ac2>bc2”的必要而不充分条件,因此③是假命题.
④∵?x∈R,f(-x)=2-x-2x=-(2x-2-x)=-f(x),∴函数f(x)=2x-2-x是奇函数,故④是真命题.
综上可知①②④是真命题.
故选C.
| 1 |
| 4 |
| 1 |
| 2 |
②当0<x<1时,lnx<0,∴?x>0,lnx+
| 1 |
| lnx |
③当c=0时,由a>b⇒ac2=bc2=0;而由ac2>bc2⇒a>b,故“a>b”是“ac2>bc2”的必要而不充分条件,因此③是假命题.
④∵?x∈R,f(-x)=2-x-2x=-(2x-2-x)=-f(x),∴函数f(x)=2x-2-x是奇函数,故④是真命题.
综上可知①②④是真命题.
故选C.
点评:本题考查了不等式及奇函数,熟练掌握以上有关知识是判断命题真假的关键.

练习册系列答案
相关题目
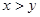 ,则
,则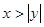 ”的逆命题
”的逆命题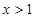 ,则
,则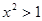 ”的否命题
”的否命题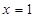 ,则
,则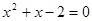 ”的否命题
”的否命题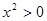 ,则
,则