题目内容
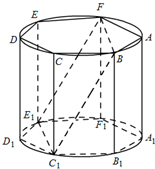 (2012•肇庆二模)如图,ABCDEF-A1B1C1D1E1F1是底面半径为1的圆柱的内接正六棱柱(底面是正六边形,侧棱垂直于底面),过FB作圆柱的截面交下底面于C1E1,已知FC1=
(2012•肇庆二模)如图,ABCDEF-A1B1C1D1E1F1是底面半径为1的圆柱的内接正六棱柱(底面是正六边形,侧棱垂直于底面),过FB作圆柱的截面交下底面于C1E1,已知FC1=| 13 |
(1)证明:四边形BFE1C1是平行四边形;
(2)证明:FB⊥CB1;
(3)求三棱锥A-A1BF的体积.
分析:(1)证明FB∥C1E1.FB=C1E1,即可证明四边形BFE1C1是平行四边形.
(2)连接FC,则FC是圆柱上底面的圆的直径,说明BF⊥BC,证明BF⊥B1B,推出BF⊥平面B1BCC1,然后证明FB⊥CB1.
(3)连接F1C1,求出三棱锥A1-ABF的高为3,求出三棱锥A1-ABF的体积,通过三棱锥A1-ABF的体积等于三棱锥A-A1BF的体积,求解三棱锥A-A1BF的体积.
(2)连接FC,则FC是圆柱上底面的圆的直径,说明BF⊥BC,证明BF⊥B1B,推出BF⊥平面B1BCC1,然后证明FB⊥CB1.
(3)连接F1C1,求出三棱锥A1-ABF的高为3,求出三棱锥A1-ABF的体积,通过三棱锥A1-ABF的体积等于三棱锥A-A1BF的体积,求解三棱锥A-A1BF的体积.
解答: (本小题满分14分)
(本小题满分14分)
证明:(1)因为圆柱的上下底面平行,
且FB、C1E1是截面与圆柱上、下底面的交线,
所以FB∥C1E1.(1分)
依题意得,正六边形ABCDEF是圆内接正六边形,
所以,正六边形的边长等于圆的半径,即AB=AF=1.((2分) )
在△ABF中,由正六边形的性质可知,∠BAF=120°,
所以,BF2=AB2+AF2-2AB•AFcos120o=2-2×(-
)=3,即BF=
((3分) )
同理可得C1E1=
,所以FB=C1E1,故四边形BFE1C1是平行四边形.(4分)
(注:本小问的证明方法较多,如有不同证明方法请参照上述证明给分)
(2)连接FC,则FC是圆柱上底面的圆的直径,∵∠CBF=90°,即BF⊥BC (6分)
又∵B1B⊥平面ABCDEF,BF?平面ABCDEF,∴BF⊥B1B (7分)
∵B1B∩BC=B,
∴BF⊥平面B1BCC1.(8分)
又∵B1C?平面B1BCC1,
∴FB⊥CB1. (9分)
(3)连接F1C1,则四边形CFF1C1是矩形,且FC=F1C1=2,FF1⊥F1C1.
在RT△FF1C1中,FF1=
=3,
∴三棱锥A1-ABF的高为3.(11分)
S△ABF=
AB•AFsin∠BAF=
×1×1×
=
(12分)
∴三棱锥A1-ABF的体积VA1-ABF=
S△ABF•FF1=
,(13分)
又三棱锥A1-ABF的体积等于三棱锥A-A1BF的体积,
∴三棱锥A-A1BF的体积等于
.(14分)
 (本小题满分14分)
(本小题满分14分)证明:(1)因为圆柱的上下底面平行,
且FB、C1E1是截面与圆柱上、下底面的交线,
所以FB∥C1E1.(1分)
依题意得,正六边形ABCDEF是圆内接正六边形,
所以,正六边形的边长等于圆的半径,即AB=AF=1.((2分) )
在△ABF中,由正六边形的性质可知,∠BAF=120°,
所以,BF2=AB2+AF2-2AB•AFcos120o=2-2×(-
| 1 |
| 2 |
| 3 |
同理可得C1E1=
| 3 |
(注:本小问的证明方法较多,如有不同证明方法请参照上述证明给分)
(2)连接FC,则FC是圆柱上底面的圆的直径,∵∠CBF=90°,即BF⊥BC (6分)
又∵B1B⊥平面ABCDEF,BF?平面ABCDEF,∴BF⊥B1B (7分)
∵B1B∩BC=B,
∴BF⊥平面B1BCC1.(8分)
又∵B1C?平面B1BCC1,
∴FB⊥CB1. (9分)
(3)连接F1C1,则四边形CFF1C1是矩形,且FC=F1C1=2,FF1⊥F1C1.
在RT△FF1C1中,FF1=
F
|
∴三棱锥A1-ABF的高为3.(11分)
S△ABF=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
∴三棱锥A1-ABF的体积VA1-ABF=
| 1 |
| 3 |
| ||
| 4 |
又三棱锥A1-ABF的体积等于三棱锥A-A1BF的体积,
∴三棱锥A-A1BF的体积等于
| ||
| 4 |
点评:本题考查棱柱、棱锥、棱台的体积,余弦定理,空间中直线与直线之间的位置关系,直线与平面垂直的判定,考查空间想象能力,计算能力.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 (2012•肇庆二模)如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1(百米).
(2012•肇庆二模)如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1(百米).