Question

已知函数在区间（-1,1）上恰有一个极值点，则实数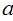的取值范围是  ____ ．

Answer 1

解析试题分析：解：由，得：
因为函数在区间（-1,1）上恰有一个极值点
所以导函数在区间（-1,1）内恰有一零点，
所以有，即： ，解得：
当时， ，令得：
当时，当时，
函数在区间（-1,1）上恰有一个极值点
所以适合题意.
当时，   ，令得： 、
当时，所以函数在区间（-1,1）上单调递减，没有极值点，
所以不适合题意.
综上：，所以答案应填：
考点：1、函数导数的求法；2、用导数研究函数的单调性与极值.