题目内容
已知非零向量 、
、 满足
满足 ,若函数
,若函数
 在R上有极值,则<a,b>的取值范围是 .
在R上有极值,则<a,b>的取值范围是 .
【答案】分析:本题可以先利用向量的数量积求出函数f(x)的解析式,即: ,然后利用极值存在,转化为开口向上的二次函数与x轴有两个交点,利用判别式△>0可解得.
,然后利用极值存在,转化为开口向上的二次函数与x轴有两个交点,利用判别式△>0可解得.
解答:解:由已知, ,
,
即 ,
,
所以
要使函数 在R上有极值,注意到f′(x)为开口向上的二次函数,所以必须且只需其判别式△>0,
在R上有极值,注意到f′(x)为开口向上的二次函数,所以必须且只需其判别式△>0,
即有:△= >0,即有:
>0,即有: 成立,得
成立,得  .
.
故答案为:
点评:本题考查了向量与函数的综合知识,考查向量的数量积以及求向量的夹角,利用函数的导数研究极值,考查函数在实数集R上的条件.
 ,然后利用极值存在,转化为开口向上的二次函数与x轴有两个交点,利用判别式△>0可解得.
,然后利用极值存在,转化为开口向上的二次函数与x轴有两个交点,利用判别式△>0可解得.解答:解:由已知,
 ,
,即
 ,
,所以

要使函数
 在R上有极值,注意到f′(x)为开口向上的二次函数,所以必须且只需其判别式△>0,
在R上有极值,注意到f′(x)为开口向上的二次函数,所以必须且只需其判别式△>0,即有:△=
 >0,即有:
>0,即有: 成立,得
成立,得  .
.故答案为:

点评:本题考查了向量与函数的综合知识,考查向量的数量积以及求向量的夹角,利用函数的导数研究极值,考查函数在实数集R上的条件.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 )·
)·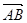 与
与 满足(
满足(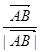 +
+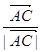 )·
)· =0,且
=0,且
 、
、 满足
满足 ,那么向量
,那么向量 与向量
与向量 的夹角为
的夹角为 B.
B. C.
C. D.
D.
 和
和 满足
满足 ,且
,且 ,
,