题目内容
若函数
在
处有定义，则“在处取得极值”是“
”的（ ）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
A
解析试题分析：根据导数的几何意义函数在处取得极值，则必有
，反之若则处不一定有极值，还要看两侧函数的单调性
考点：函数极值及充分条件必要条件
点评：若
则
是
的充分条件，是的必要条件，函数在极值点处的导数为零
练习册系列答案
相关题目
命题“
”的否定是
A． | B． |
C． | D． |
”的否定是 。有下列四个命题，其中真命题有：（ ）
①“若
，则
．
互为相反数”的逆命题
②“全等三角形的面积相等”的否命题
③“若
，则
有实根”的逆命题
④“不等边三角形的三个内角相等”的逆否命题，其中真命题的序号为：
| A．①③ | B．②③ | C．①② | D．③④ |
是
的
| A．必要而不充分条件 | B．充分而不必要条件 |
| C．充要条件 | D．既不充分也不必要条件 |
已知命题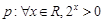
，那么命题
为
A． | B． |
C． | D． |
有意义; （2）函数是其定义域到值域的映射;
的图象是一直线；（4）函数
的图象是抛物线，命题“
”的否定是( )
A． | B． |
C． | D． |
下列命题中，是真命题的是（ ）
A． | B． |
C． | D． |