题目内容
在正方体ABCD—A1B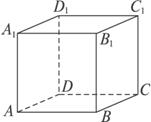
证明:连结NM、MH、HG、GN、AC、NE、EH、FG,
∵N、H分别为DA、DC的中点,∴MH∥AC.
∵N、G分别为AA1、CC1的中点,∴AC∥NG.∴MH∥NG.
∴N、M、H、G四点共面.
同理,MN∥HE,
∴N、M、H、E四点共面.
∵平面NMHG与平面NMHE都经过不共线的三点N、M、H.
∴平面NMHG与平面NMHE是同一个平面.
∴E在平面NMHG内.
同理,可证平面FGHE与平面NMHG是同一个平面.
∴F在平面NMHG内.
∴E、F、G、H、M、N六点共面.
练习册系列答案
相关题目
16、在正方体ABCD-A′B′C′D′中，过对角线BD′的一个平面交AA′于E，交CC′于F，则
如图，在正方体ABCD-A′B′C′D′中，E，F分别是AB′，BC′的中点． 
如图在正方体ABCD-A 1B1C1D1中，O是底面ABCD的中心，B1H⊥D1O，H为垂足，则B1H与平面AD1C的位置关系是（ ）