题目内容
在△ABC中，a、b、c分别是角A、B、C所对的边，满足a2+c2-b2=ac．
（1）求角B的大小；
（2）设
=（sinA，cos2A），
=（-6，-1），求
的最小值；
（3）若x∈[0，π），求函数f（x）=sin（x-B）+sinx的值域．
解：（1）在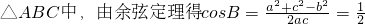 
又∵B∈（0，π），∴
；
（2）=-6sinA-cos2A=-6sinA-（1-2sin2A）=2（sinA-
）2-
∵0＜sinA＜
∴0＜sinA≤1当sinA=1时取最小值，为-5
（3）
∵
∴
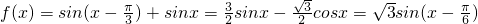
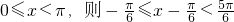
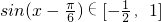
故函数f（x）的值域为[-
，
]
分析：（1）利用余弦定理求得cosB，进而求得B．
（2）利用两角和公式对函数f（x）的解析式化简整理，进而根据正弦函数的性质求得函数的值域．
（3）首先将函数化简f（x）=sin（x-B）+sinx=sin（x-
），然后由x的范围确定x-的范围，进而得出sin（x-）的值域，即可得出结果．
点评：本题主要考查了余弦定理的运用、正弦函数定义域和值域，解题过程中尤其要注意角的范围．属基础题．
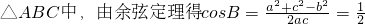
又∵B∈（0，π），∴
；（2）
=-6sinA-cos2A=-6sinA-（1-2sin2A）=2（sinA-）2-∵0＜sinA＜
∴0＜sinA≤1当sinA=1时取最小值，为-5
（3）
∵
∴
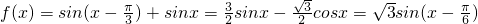
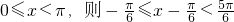
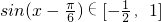
故函数f（x）的值域为[-
，]分析：（1）利用余弦定理求得cosB，进而求得B．
（2）利用两角和公式对函数f（x）的解析式化简整理，进而根据正弦函数的性质求得函数的值域．
（3）首先将函数化简f（x）=sin（x-B）+sinx=
sin（x-），然后由x的范围确定x-的范围，进而得出sin（x-）的值域，即可得出结果．点评：本题主要考查了余弦定理的运用、正弦函数定义域和值域，解题过程中尤其要注意角的范围．属基础题．
练习册系列答案
相关题目
在△ABC中，∠A、∠B、∠C所对的边长分别是a、b、c．满足2acosC+ccosA=b．则sinA+sinB的最大值是（ ）
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|